PhD Mouchkaev A.S.^*, DSc. L'vov A.A., PhD L'vov P.A., and Matoshko I.M.

^*Korea Advanced Institute of Science and Technology, Daejeon, South Korea

Saratov State Technical University named after Gagarin J.A., Saratov, Russia

Radio Frequency Identification using Multi-port Junction

Radio frequency identification (RFID) system is a wireless communication system in which the radio link between the base station (reader) and the transponders is provided by the modulated backscattered waves. The reader sends information to one or more transponders by amplitude-shift keying (ASK) modulating an RF carrier. The transponder responds by ASK/PSK (phase-shift keying) modulating the impedance placed on the antenna terminals. In doing so, it backscatters an information signal to the reader. The read/write range performance of a RFID system depends mainly on the choice of frequency, radiated power from the reader, sensitivity and modulation efficiency of a transponder, data rate, reader receiver sensitivity in the presence of self-jammer signal and location of the transponder [1].

The biggest challenge for the receiver front-end is to handle leakage from the full power continuous wave (CW) signal being transmitted during reception to keep the passive transponders powered up. This calls for the design of a wide dynamic range receiver or a use of some sort of an isolation approach, or self-jammer cancellation technique. However, the isolation between transmitting and receiving channels increases the RFID reader cost. Leakage canceller complicates the reader receiver and adds to the reader’s consumption that is critical for mobile applications.

In this paper, a new demodulation method is proposed which utilizes the leakage signal instead of its canceling. The method is based on the multi-port reflectometer direct conversion technique and allows estimating phase of the received signal with respect to the phase of transmitting CW signal (Fig.1).

The multi-port reflectometer is a measurement device that allows measuring both the amplitude ratio and the phase difference of two electromagnetic waves [2]. The use of this device in RFID reader receiver is justified as the multi-port reflectometer measures the so-called complex reflection coefficient of a device under test (transponder), i.e. the ratio of the wave reflected by the transponder to the wave incident to the transponder. Therefore, both amplitude and phase information can be estimated. In the multi-port reflectometer, information of phase is obtained by making only power measurements of several different linear combinations of the two electromagnetic waves (reference and backscattered). This means that a multi-port reflectometer is a passive linear circuit with two input ports and N ≥ 4 output (measuring) ports, which provides at its outputs N different linear combinations of the waves present at its inputs [2].

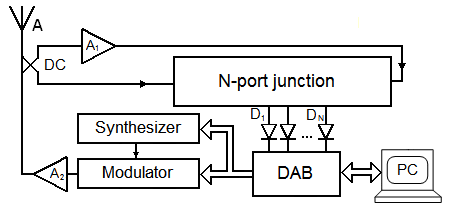
Fig.1. A is antenna; A₁, A₂ are amplifiers; DC is directional coupler; D₁,...D_N are detectors;
DAB is data acquisition board; PC is personal computer.

Consider the system model of the multi-port circuit two input ports of which connected to transmitted and coupled ports of a directional coupler. The multi-port circuit performs additive direct conversion of input mixture signals containing the signal backscattered by the transponder and the leakage signal from the transmitter. Digitized signalat i-th power sensor (detector) output is represented by the following model [3]:

, , (1)

where are complex gains of i-th sensor; are k-th samples of complex amplitudes of the leakage and the received signal, respectively; is k-th sample of additive white Gaussian noise at i-th sensor, N is the number of measuring ports. The complex gains of the power sensors are unknown and entitled to be found. The complex amplitudes are unknown as well, however, in our case we need to estimate the relative phase between named complex waves at time moment k. We assume that are constant during the transponder response, but the complex amplitude and vary as there are short-term frequency variation and frequency drift of the transponder signal resulting in phase variation [1]. The equation (1) can be expressed as

, (2)

where is the phase angle between and .

First, bearing in mind physical properties of signals and we simplify (2). Since the backscattered signal is much weaker than the leakage, i.e. , the second term in (2) can be neglected:

, (3)

The second assumption is that the sample size at every multi-port output K is rather large (gross sample). Averaging for each sensor in (3) (it can be done during preamble of the received signal after bit synchronization [5]) results in

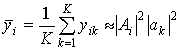, , (4)

since a sum harmonic series with random phase tends to zero, provided K is large enough. Then, after the next transformation

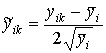, , (5)

the set of equations (3) can be written as

, , (6)

where .

After the following variable substitution:

, (7)

the set (6) can be represented as:

, . (8)

The estimates of unknown parameters can be found by the maximum likelihood (ML) method [6]. The assumption of Gaussian distribution of measuring errors is quite natural, because they occur largely due to the shot noise of the power sensors and thermal noise of the DAB amplifiers. Hence, the values of have the same distribution as well. Therefore, the ML estimates of the parameters under consideration is obtained by solving the nonlinear least squares problem [6]:

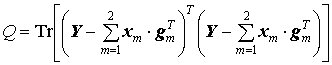(9)

where is the data matrix (K×N) containing the values from (5); and are vectors of the size K and N containing the values and from (7) respectively; operators Tr and ^T designate the trace of matrix and the transpose matrix respectively.

It is shown [6] that the solution of problem (9), i.e. vectors delivering the global minimum to Q, should have the following form

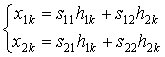(10)

where h_1k and h_2k are the components of eigenvectors corresponding to two largest eigen values of matrix (K´K). So, the nonlinear problem (9) is substituted by the equivalent linear one (10). And four unknown constants s₁₁ ,..., s₂₂ can be determined using the next consideration.

From physical point of view, as distances between the reader and tags vary in the range exceeding several wavelength of the reference signal and frequency tolerance of the tags is high, one can assume that distribution of the measuring phases j_k (k=1,...,K) is uniform in the segment [0,2π]. In case of accurate estimates of the phases (constants s₁₁ ,..., s₂₂ are determined correctly), their distribution got from expression is uniform either.

Let us suppose that incorrect estimators of constants s₁₁ ,..., s₂₂ differing from their true values are found. Then calculation of parameters' estimates and from (10) will be equivalent to some linear transformation of the true values , and the distribution of phase estimates will differ of uniform one. Hence, if we evaluate this distribution (e.g. with the help of the frequency diagram of the phase estimates dividing the whole segment [0,2π] into r bins) then it should be compared with the universal one and some correction factors for constants s₁₁ ,..., s₂₂ could be calculated.

Assume that in equation (10) s₁₁ = s₂₂ = 1, and s₁₂ = s₂₁ = 0. Then the calculation of estimates gives , and . The histogram construction (Fig. 2) shows that the distribution of the phases differs of uniform. That is why, the correction factors is to be calculated from the expressions:

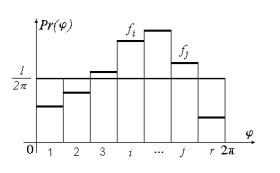
Fig.2. Histogram of the phase estimates.

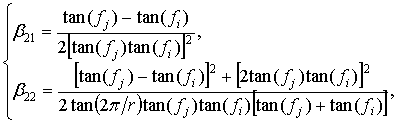(11)

where f_j and f_i are relative rate of entering any two bins i and j from the set of r bins [5]. Subsequently, the estimates of can be found as

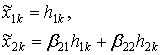_, (12)

and finally

(13)

Thus, it becomes possible to measure the phase sequence coming from the tag without precise calibration of the multi-port reflectometer.

Fig. 3 demonstrates the simulation results of phase measuring with the multi-port technique and assures the effectiveness of the proposed approach, since the required amount of precise instrumentation can be reduced drastically.

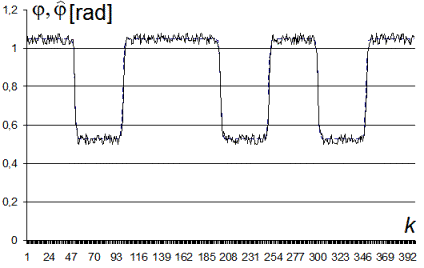
Fig. 3. – Real phases (dashed line) and their estimates (solid line) – as function of discrete time.

REFERENCES:

1. K. Finkenzeller, RFID Handbook: Fundamentals and Applications in Contactless Smart Cards and Identification. New York: Wiley, 2003.

2. A. L'vov, A. Mouchkaev, “A New Technique for Measuring the Scattering Parameters of Two-Port Junctions with Single Multiport Reflectometer”. 47thARFTG Conference Digest-Spring, pp.181-187, 1996.

3. G.F. Engen, "The six-port reflectometer: An alternative network analyzer," IEEE Trans. Microwave Theory Tech., vol. MTT-25, pp. 1075-1080, Dec. 1977.

4. EPC^TM Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID. Protocol for Communications at 860-960 MHz., ver. 1.2.0., 2008.

5. A. Muchkaev, A. L’vov, N. Danilov, O. Kolesnikova, “Six-port calibration in the RFID reader receiver,” in Proc. 24-th Int. Confer. Math.Methods in Engin.&Tech., Saratov, Kiev, Penza, Apr.-Sep., 2011.(in Russian)

6. A. L'vov, K. Semenov. “A Statistical Calibration Technique of the Automated Multi-probe Transmission Line Reflectometer,” in Proc. of the 10th Int. Confer. "Systems for Automation of Engineering and Research", September 27- 29, 1996, St. Konstantin, Bulgaria, P. 38-42.