К.ф-м.н., доц. Гусев А.Ю., Обора И.О.

ГВУЗ «Национальный горный университет», Днепропетровск

Исследование стохастических характеристик IP – трафика

В настоящей работе исследованы основные статистические характеристики IP-трафика Ethernet - сети ГВУЗ «НГУ» г. Днепропетровска и определена степень его фрактальности. На основании экспериментального исследования показано, что трафик обладает свойством самоподобия с показателем Хэрста 0,601.

Ключевые слова: Пакетный трафик, спектральный анализ, автокорреляционная функция, спектральная плотность, фрактал, медленно убывающая зависимость, быстро убывающая зависимость.

Введение

Многочисленные исследования пакетного трафика компьютерных сетей свидетельствуют о том, что он имеет особую фрактальную структуру. При этом, в процессе передачи могут возникать большие всплески при относительно низком среднем уровне трафика. Данное явление, значительно влияющее на потери и задержки пакетов, не учитывается классической теорией телетрафика. Поэтому, расчеты параметров системы, предназначенной для обработки сетевого трафика классическими методами теории массового обслуживания, дают некорректные, неоправданно оптимистические результаты, поскольку алгоритмы обработки трафика, созданные для работы с простейшим потоком, неэффективны для фрактальных потоков. Таким образом, необходимость обеспечения высокого качества обслуживания сетей с пакетным трафиком обусловливает актуальность исследования его статистических характеристик с целью создания эффективных алгоритмов обработки.

Постановка задания. Исследования пакетного трафика показали, что это фрактальный процесс и для его описания традиционные марковские модели с кратковременной памятью некорректны. Поэтому для повышения качества обслуживания (QoS) необходимо решение задачи исследования свойств самоподобия современного трафика компьютерных сетей. В работе представлены результаты статистического анализа пакетного IP-трафика.

Цель статьи. Исследование структуры IP-трафика, направленное на выявление его характерных особенностей и расчет основных статистических характеристик.

1. Реализация сетевого трафика

Для исследования выбрана одна из реализаций сетевого трафика, полученная в лабораторных условиях ГВУЗ «НГУ» г. Днепропетровска. Измерения проводились на протяжении 20 рабочих дней. Получено свыше 50000 отсчетов (для исследования было взято 16000 отсчетов). Измерялось количество принятых и переданных IP-пакетов объемом 10 Gb. В схеме эксперимента использованы ADSL-доступ (100 Mbps, Ethernet) и операционная система Linux.

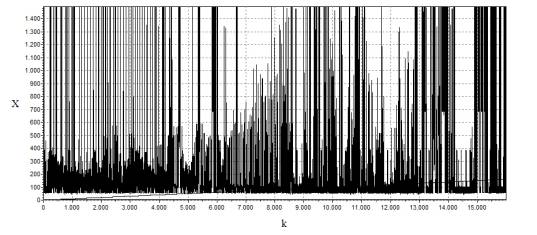
Рисунок 1. Вид исследуемой реализации трафика

2. Анализ автокорреляционной функции

Рассмотрим, обладает ли временной ряд медленно убывающей зависимостью

(МУЗ) или быстро убывающей зависимостью (БУЗ). Процесс с МУЗ характеризуется автокорреляционной функцией, которая убывает по степенному закону при увеличении временной задержки (лага). В отличие от процесса с МУЗ, процесс с БУЗ обладает экспоненциально спадающей автокорреляционной функцией (АКФ). Вычисление АКФ выполнено с помощью программы Fractan 4.4 по формуле:

,

где - выборочное среднее ряда , выборочная дисперсия ряда ,

Автокорреляционная функция временного ряда приведена на рисунке 1. Это колебательный процесс, который не обращается в нуль при больших значениях k, что говорит о медленном убывании АКФ и присутствии МУЗ в исследуемом трафике.

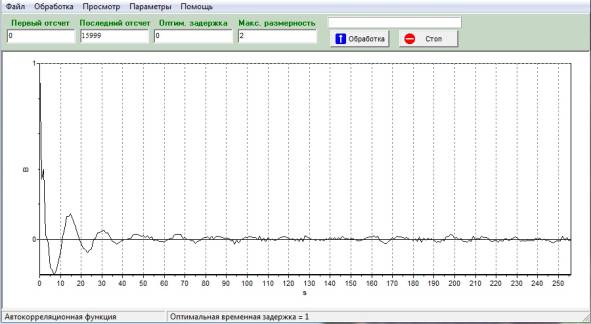
Рисунок 2. АКФ временного ряда

3. Спектральный анализ

Рассчитаем энергетический спектр исследуемого временного ряда. Известно [1], что в частотной области МУЗ приводит к степенному закону поведения спектральной плотности процесса. Процесс обладает МУЗ, если для спектральной плотности выполняется , где , , и - медленно изменяющаяся в нуле функция, const.

Таким образом, с точки зрения спектрального анализа процесс с МУЗ обладает спектральной плотностью с особенностью в нуле (т.е. спектральная плотность такого процесса стремится к бесконечности, по мере того как частота стремится к нулю). Такой процесс часто называют « – шум» или «фликкер-шум».

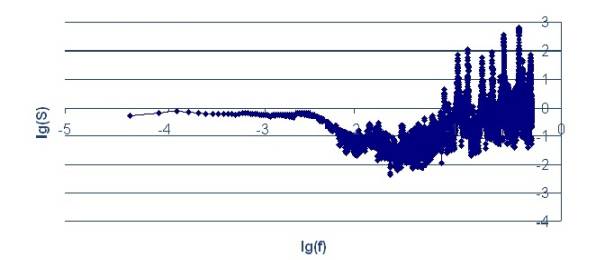
Рисунок 3. Спектральная плотность

4. Расчёт фрактальных параметров

Показатель (коэффициент Хэрста) [1] связан с ранее рассмотренным при изучении АКФ параметром (корреляционный параметр) следующим соотношением:

Спектральный показатель b рассчитывается по формуле:

Фрактальный показатель рассчитывается по формуле:

Корреляционная размерность рассчитывается по формуле:

Или с помощью программы Fractan 4.4. (рис.4).

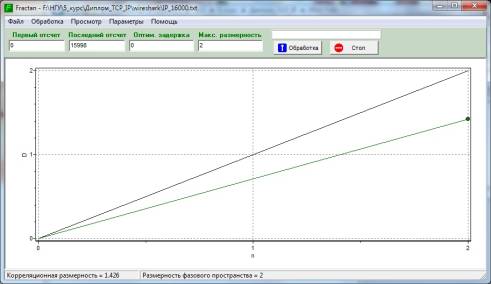
Рисунок 4. Определение корреляционной размерности

Выводы

В данной работе для исследования IP-трафика выполнен анализ автокорреляционной функции и энергетического спектра. Выполнен расчет фрактальных параметров.

Получены следующие результаты:

1. Изучаемый временной ряд не подчиняется нормальному распределению.

2. Изучаемый временной ряд не обладает экспоненциально спадающей АКФ, свойственной случайным процессам.

3. Изучаемый временной ряд обладает свойством самоподобия с коэффициентом Хэрста 0,601.

Перспективным направлением дальнейших исследований может быть анализ сетевых процессов методами нелинейной динамики. Для повышения эффективности работы современных телекоммуникационных систем требуется создание математических моделей, наиболее полно отражающих фрактальные свойства сетевых процессов.

Литература:

1. Столлингс В. Современные компьютерные сети. - СПб.: Питер, 2003. -783 с.