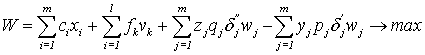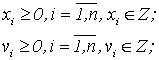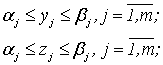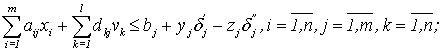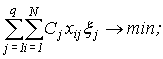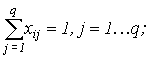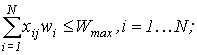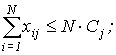Математика/ 5. Математичне моделювання

Скрильник І.І., Масюк В. В.

Полтавський національний технічний університет, Україна

Економіко-математична модель оптимізації виробництва

Оптимізаційні методи й моделі математичного програмування і дослідження операцій знайшли широке використання для розв’язування різноманітних задач економіки. Довільна оптимізаційна модель містить, як правило, дві складові: цільову функцію, обмеження. Цільова функція формалізує критерій оптимальності, за яким серед допустимих планів вибирається якнайкращий, а обмеження щодо змінних визначають множину допустимих планів.

Найпоширенішими прикладами економічних задач лінійного програмування є задача про оптимальний розподіл виробничих ресурсів із неперервними змінними, що показують обсяги виробництва продукції, транспортна задача тощо. Розглянемо задачу оптимізації виробництва при можливості додаткового придбання сировини та реалізації її лишків.

Постановка задачі. Нехай деяке підприємство може випускати кілька видів готової продукції та напівфабрикатів, використовуючи для цього певні види сировини. При необхідності підприємство може придбати за встановленими цінами додаткову сировину або продати залишки сировини, при чому, ціна закупки та продажу сировини залежатиме від її якості. Потрібно розробити план виготовлення продукції підприємства, придбання та реалізації сировини, який забезпечив би для нього найбільший прибуток. Виготовлену продукцію за визначеним планом потрібно оптимально розмістити по контейнерам із встановленими вартостями.

Відомі параметри моделі: n – кількість видів сировини; j – індекс сировини; m – кількість видів продукції; i – індекс продукції; – запас j-ї сировини; – кількість j-ї сировини, яка потрібна для виготовлення одиниці i-ї готової продукції; – кількість k-ї сировини, яка потрібна для виготовлення одиниці j-го напівфабрикату; – прибуток від реалізації одиниці i-ї готової продукції; – прибуток від реалізації одиниці k-го напівфабрикату; – ціна придбання одиниці j-ї сировини; – ціна реалізації j-ї сировини (може бути або ); – нижня та верхня межі для придбання та реалізації сировини; – ціновий коефіцієнт на якість сировини.

Керовані параметри: – кількість i-ї продукції, що заплановано випустити; – кількість додатково придбаної j-ї сировини; – кількість реалізованої j-ї сировини; – кількість запланованих напівфабрикатів; – індикатор придбання сировини (дорівнює 0, якщо ми не купуємо сировину і 1, якщо купуємо її); – індикатор реалізації сировини (дорівнює 0, якщо ми не продаємо сировину і 1, якщо продаємо її).

Критерієм розв’язку задачі є загальний прибуток, який позначимо . З урахуванням взаємозалежностей між керованими змінними, некерованими параметрами та відомими величинами економіко-математична модель цієї задачі набуває такого вигляду:

	(1)
	(2)
	(3)
	(4)
	(5)

Розв’язком задачі є план виготовлення готової продукції видів та план виготовлення напівфабрикатів видів, що становлять загальну кількість N видів випущеної продукції.

Потрібно розв’язати логістичну задачу оптимального розміщення готових видів продукції підприємства по контейнерах, що мають певну вартість.

Відомі параметри моделі: – кількість видів випущеної продукції підприєством; – кількість продукції, що випущено по кожному виду; j – індекс контейнера; i – індекс виду продукції; – вартість j-го контейнера; – місткість j-го контейнера; q – кількість контейнерів.

Керовані параметри: – індикатор розміщення готових видів продукції у контейнері; – i-й вид продукції, що розміщений в j-му контейнері.

Для розв’язання задачі використаємо пофарбування графової моделі. Нехай кожний вид випущеної продукції співвідноситься з деякою вершиною графа G. Кожний раз, коли два види та () не можуть бути розміщені в одному контейнері (пофарбовані в однаковий колір), у граф G вводиться ребро . Поставимо вершинам графа у відповідність ваги. Оптимально розмістити види випущеної продукції по контейнерам – це означає пофарбувати вершини графа G у найменшу кількість кольорів із множини . Кількість елементів у множині не повинно перевищувати верхню оцінку хроматичного числа , що визначається за формулою

,

(6)

де означає степінь і-ої вершини . Тоді задача буде мати наступний вигляд:

	(7)
	(8)
	(9)
	(10)
	(11)
	(12)

Для пофарбування теоретико-графової моделі, що відповідає задачі, можна використати метод 0-1 програмування. У такому формулюванні задачі змінна набуває значення “1”, якщо в контейнер j можна помістити вид випущеної продукції, і дорівнює “0” в іншому разі. Обмеження (9) гарантує, що будь-які суміжні вершини і пофарбовані в різні кольори, обмеження (10) означає, що жодний із контейнерів не перевантажується, а обмеження (11) гарантує виконання умови: якщо , тобто якщо j-й контейнер порожній, то всі також дорівнюють нулю.

Література:

1. Кігель В. Р. Математичні методи ринкової економіки / В. Р. Кігель. – К: Кондор, 2003. – 158 c.

2. Кристофидес Н. Теория графов. Алгоритмический подход / Кристофидес Н. – М: Мир, 1978. – С. 75 – 94.

3. Connolly D. General Purpose Simulated Annealing / D. Connolly // The Journal of the Operational Research Society: Mathematical Programming in Honour of Ailsa Land. – 1992. – V. 43, № 5. – P. 495 – 505.

4. Abramson D. A Simulated Annealing Code for General Integer Linear Programs / D. Abramson, M. Randall // Annals of Operations Research. – 1999. – V. 86, P. 3 – 24.