УДК 517.9
Линизированная система уравнении
Навье - Стокса.
А.П. Мустафаев
Семипалатинский государственный
университет имени Шакарима.
Навье – Стокс уравнение – дифференциальные
уравнения движения вязкой жидкости (газа) названы по имени Л.Навье и Дж. Стокса.
Для несжимаемой (плотность ![]() ) и ненагреваемой (температура t- const) уравнения Навье – Стокса в проекциях на оси
прямоугольной декартовой системы координат (система трех уравнений) имеет вид
) и ненагреваемой (температура t- const) уравнения Навье – Стокса в проекциях на оси
прямоугольной декартовой системы координат (система трех уравнений) имеет вид
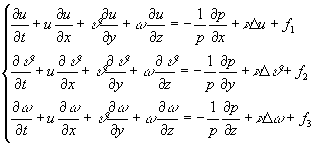 (1)
(1)
Здесь t- время, x, y, z – координаты жидкой частицы, ![]() - проекции ее скорости,
- проекции ее скорости, ![]() - проекции объемной
силы,
- проекции объемной
силы, ![]() - кинематический
коэффициент вязкости, m- динамический коэффициент вязкости, p- давление.
- кинематический
коэффициент вязкости, m- динамический коэффициент вязкости, p- давление.
Чтобы
замкнуть систему, к уравнениям (1) присоединяют уравнения неразрывности имеющий
для несжимаемой жидкости вид
![]() (2)
(2)
До
сих пор решение этих уравнений найдены лишь в некоторых частных случаях. В
настоящее время существует несколько ситуации (обусловленных простой геометрий)
которые решены аналитическом виде. В остальных случаях используется численные
моделирования, поэтому нет полного понимания свойств уравнения Навье – Стокса.
Здесь
неизвестными величинами является скорости ![]() ,
, ![]() ,
, ![]() и давление
и давление ![]() .
.
В частности эти функции удовлетворяют
линейной системе уравнении с частными производными Навье – Стокса.
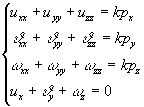 (3)
(3)
В настоящей работе мы покажем, что частный
вид общего решения этой системы можно получить через вполне определенные
функции.
Пусть ![]() , тогда имеем систему вида
, тогда имеем систему вида
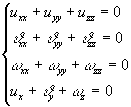 (4)
(4)
При предложении непрерывной дифференцируемости ![]() до третьего порядка
система (4) равносильна системе
до третьего порядка
система (4) равносильна системе
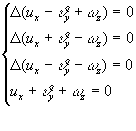 (5)
(5)
где ![]() - оператор Лапласа.
- оператор Лапласа.
Далее с помощью замены
![]() (6)
(6)
уравнения Лапласа приводится к дифференциальному
уравнению вида
![]() (7)
(7)
где ![]()
![]() .
.
Решая это уравнение и переходя к старым переменным x,y,z имеем
![]() (8)
(8)
Аналогично, решая остальные уравнения системы (5)
учитывая (2), (8) имеем
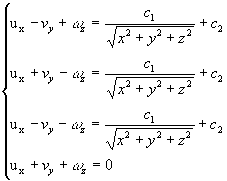 (9)
(9)
Тогда решение системы (3) при p=const имеет вид
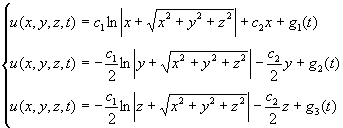 (10)
(10)
где ![]() - произвольные
постоянные,
- произвольные
постоянные, ![]() - произвольные
функции.
- произвольные
функции.
Правильность полученных решении легко
можно проверить, подставляя (10) в (3).
Литература:
1.
А.В. Бицадзе. Некоторые
классы уравнений частных производных. – М.:, Наука, 1981.
2.
А.П. Мустафаев.
Некоторые частные решения уравнения Лапласа. Материал ІV международной научной практической конференций.
«Научная мысль информационного века.- 2008» Том 13. Publishing House “Education and
Science” S.p.o Прага (Чехия).