Экономические науки / 8. математические методы в экономике

Дмитренко И.С.

Донбасская государственная машиностроительная академия

Применение комбинации методов классической оптимизации и графоаналитических методов при решении задач исследования операций

Значительное число задач исследования операций, возникающих в обществе, связано с сознательно управляемыми явлениями и такими, что для их планирования и управления имеется достаточно большое число различных вариантов решения. На практике каждый раз приходится рассматривать огромное число различных вариантов решения одной и той же задачи, отбрасывая одни и принимая другие. Естественно, различные варианты плана требуют неодинаковых затрат и дают, наконец, неодинаковый экономический эффект. Доказательство эффективности, иногда трудно произвести аналитическим путем и тогда этот путь приходится проделывать с помощью графической интерпретации процесса решения.

Для иллюстрации такой специфической позиции в процессе обучения специалистов- экономистов, рассмотрим следующую учебную задачу.

Два завода по производству однородной продукции производят в сутки 3000 единиц данной продукции. Затраты на производство выражаются квадратичными зависимостями: и , где - количество единиц продукции, производимых на 1-ом и 2-ом заводе соответственно. Определить необходимое количество производства на 1-ом и 2-ом заводе из условия минимума суммарных затрат.

Данная задача представляет собой задачу на определение условного экстремума функции нескольких переменных. Для ее решения логично использовать классические условия Куна - Таккера с составлением функции Лагранжа:

Применяя соответствующие условия, получим оптимальную точку B(1750, 1250) и значение целевой функции в ней F(1750, 1250)= 8875000 ден.ед.

Однако доказательство экстремума не было проведено, т.к. для получения таких результатов были использованы только необходимые, а не достаточные условия экстремума. Одним из приемов подобного доказательства является графический метод решения задачи.

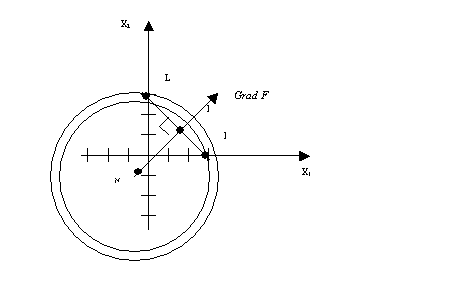
Докажем наличие минимума путем геометрического построения множества допустимых решений задачи и линий уровня целевой функции. Для этого построим линии уровня, являющиеся в данном случае окружностями с центром в точке N(-500, -1000), и градиент целевой функции в точках M(3000;0) и L(0;3000). Так как градиент целевой функции направлен во внешность окружностей, то минимума целевая функция достигает в той точке, в которой линия уровня касается прямой . Для нахождения координат соответствующей точки составим уравнение прямой NB, перпендикулярной прямой и проходящей через точку N(-500, -1000). Найдем координаты точки пересечения прямой и прямой NB: . Таким образом, экстремального значения целевая функция достигает в полученной точке пересечения прямых - точке B. Это значение составляет8875000ден.ед.

Сравнивая результаты, полученные путем геометрического и аналитического решения задачи, заметим, что результаты совпадают, но графическое решение дает нам достаточные условия доказательства экстремума.

Отметим, что геометрическая наглядность является более «иллюстративным» способом обучения студентов и дальнейшим прогрессивным методом исследования различных экономических ситуаций в реальной сфере деятельности будущего специалиста- экономиста. Так, применяя сначала в учебных целях оба метода в комбинации либо графический метод в отдельности, а затем - в производственных целях, специалист экономического направления всегда сможет принять правильное, математически обоснованное решение.

Литература:

1. Сборник задач и упражнений по высшей математике: Мат. программирование: Учеб.пособие / А.В.Кузнецов, В.А.Сакович, Н.И.Холод и др.; 2-е изд.,перераб. и доп.- Мн.:Выш.шк.,2002. 271-278с.

2. Дмитренко И.С. Сведение задачи планирования предприятия к задаче нелинейного программирования. Materialy 6 miedzynarodowej naukowi-praktycznej konferencji " Naukowa przestrzec europy-2010" 07-15 kwietnia 2010 roku, volume 6, ekonomiczne nauki, Przemysl, Nauka i studia 2010, стр. 58-61