Математика/1
Замковая Л.Д.
Национальный
горный университет (Украина)
о практической устойчивости
интегро-дифференциальных систем относительно
части переменных
Введение.
Математической
моделью динамики некоторых механических, экологических и других систем являются
интегро-дифференциальные уравнения. Важное место при качественном анализе
поведения решений таких систем вместе с устойчивостью по Ляпунову по всем
переменным занимает свойство практической устойчивости по части переменных.
Задачи устойчивости по части переменных естественным образом возникают при
решении ряда технических проблем, анализе биологических и экономических моделей
[1-3]. Основные результаты исследования
устойчивости по части переменных решений систем дифференциальных уравнений
приведены в обзоре [2]. Здесь же отмечено, что к одному из важных направлений
исследования устойчивости по части переменных различных классов уравнений
относится изучение практической устойчивости [4-5] по части переменных.
Настоящая статья
посвящена установлению достаточных условий практической устойчивости по части
переменных решений квазилинейных дифференциальных систем, содержащих степенные
и интегральные возмущения. При этом предполагается, что известны оценки матриц
Коши системы линейного приближения. Для доказательства применяется метод
интегральных неравенств.
Постановка
задачи. Рассматривается система
двух уравнений, одно из которых является дифференциальным, а второе –
интегро-дифференциальным.
, (1)
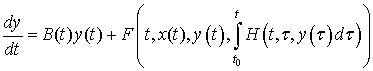, (2)
где 
; 
; 
– матрица; 
,
– матрица;
; 
; 
.
Предполагается,
что система (1), (2) имеет единственное решение 
, 
, удовлетворяющее условию 
, 
и существующее при
всех 
. Кроме того,
.
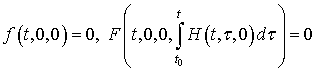Нелинейной системе (1), (2) поставим в соответствие систему линейного приближения (3), (4):
, (3)
. (4)
Относительно линейной системы (3), (4) и возмущений f и F делаются следующие предположения.
Предположение
1. Матрица Коши 
системы (3) и 
системы (4) при 
удовлетворяют
неравенствам
, (5)
(6)
с некоторыми
положительными функциями 
, 
, 
, 
.
Предположение
2. Вектор функции 
, 
, 
в области 
удовлетворяют
неравенствам
, 
, (7)
, (8)
, (9)
где 
, 
, 
; 
, 
, 
, 
– неотрицательные
непрерывные функции при 
.
Здесь
и далее 
– любая векторная
норма в 
.
Цель
данной статьи: установить достаточные условия практической устойчивости по
части переменных нулевого решения 
, 
системы (1), (2) при
предположениях 1 и 2.
Сформулируем
определение практической устойчивости по части переменных согласно [4, с. 47].
Определение.
Решение 
, 
системы (1), (2)
называется 
практически y-устойчивым, если при любых значениях 
, 
, для которых 
и 
; 
и 
для нормы решения 
выполняется оценка 
при всех 
.
Основные
результаты статьи. Введем обозначения.
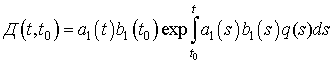, (10)
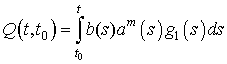, (11)
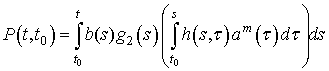. (12)
Теорема 1. Пусть:
1) выполняются
предположения 1 и 2, где 
;
2) существуют
величины 
, 
, 
, 
такие, что при 
:
, (13)
,
, (14)
, (15)
где 
, Q, P определены в (10), (11), (12);
3) величины 
и А удовлетворяют соотношению
.
Тогда решение 
, у = 0 системы (1), (2) 
практически y-устойчиво.
Теорема 2. Пусть:
1) выполняются
предположения 1 и 2, где 
;
2) выполняется
условие 2) теоремы 1;
3) 
, (15)
где
; (16)
4) величины 
и А
удовлетворяют соотношению
.
Тогда нулевое решение 
, 
системы (1), (2) 
практически у-устойчиво.
Доказательство. Покажем, что при выполнении условий (5), (7)
и (13) решение 
первого из уравнений
системы (1), (2) удовлетворяет оценке
. (17)
Исходя из
формулы Коши для 
,
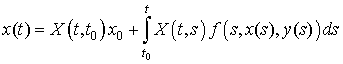используя
неравенства (5) и (7), получим
.
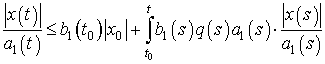Отсюда, в силу
леммы Гронуолла-Беллмана, обозначения (10) и условия (13), устанавливаем оценку
(17):
.
Далее получим
оценку решения 
второго из уравнений
системы (1), (2). Формула Коши для 
имеет вид
.
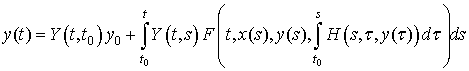На основании
условий (6), (8), (9) и оценки 
(17) получаем
.
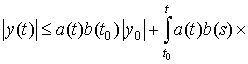
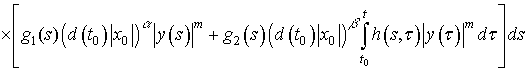Запишем это
неравенство в виде
.
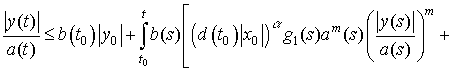
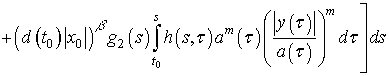Оценим решение
этого неравенства согласно [6]. Получим:
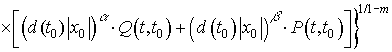при 
;
при 
,
при условии, что выражение в
фигурных скобках положительно. Здесь 
и 
определены в (11),
(12).
Используя
условия (14) и (15),получаем следующие оценки решения 
.
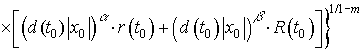при 
. (18)
, 
, (19)
если 
,
.
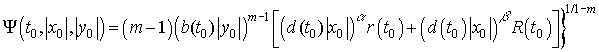(20)
Заметим, что
оценки (18) и (19) установлены при выполнении условий 1) и 2) соответственно
теорем 1 и 2.
Обозначим правую
часть неравенства (18) через 
. Пусть теперь 
, 
. Тогда в силу монотонного возрастания функции 
по 
и 
получаем
, 
.
Из этого
неравенства и условия 3) теоремы 1 следует, что если 
и 
, то 
при всех 
. Теорема 1 доказана.
Рассмотрим
теперь оценку (19) решения 
, соответствующую значениям 
. Возьмем начальные условия из области 
, 
. В силу монотонного возрастания функции 
(20) по 
и 
, обозначения 
(16) и условия 3)
теоремы 2 имеем:
, (21)
т.е. при 
, 
справедлива оценка
(19).
Из (19), (21) и
условия 4) теоремы 2 следует, что если 
и 
, то
, 
.
Теорема 2
доказана.
Анализ
полученных результатов. В [4, теорема 7.10] установлен
достаточный признак практической устойчивости по части переменных системы (1),
(2), в которой 
, т.е. интегральные возмущения отсутствуют, а для матриц Коши
системы линейного приближения (3), (4) и нелинейностей 
и 
выполняются условия: 
, 
, 
, 
, 
– const; 
, 
, 
, 
, 
и 
– некоторые
положительные функции.
Настоящая статья
представляет собой развитие первого метода Ляпунова при изучении практической
устойчивости по части переменных решений дифференциальных систем, содержащих
степенные и интегральные возмущения.
Литература
1. Воротников В.И., Румянцев В.В. Устойчивость и
управление по части координат фазового вектора динамических систем: Теория,
методы и приложения. М.: Научный мир, 2001. 320 с.
2. Воротников В.И. Частичная устойчивость и
управление // Автоматика и телемеханика. – 2005. – №4. – с. 3–59.
3. Вольтерра В. Математическая теория борьбы за
существование. М.: Наука, 1976. 286 с.
4. Мартынюк А.А. Практическая устойчивость движения.
К.: Наукова думка, 1983. – 248 с.
5. Мартынюк А.А. О некоторых результатах развития
теорий устойчивости движения: классических и современных // Прикладная
механика. – 2001. – 37, №9. – с. 44–60.
6. Филатов
А.Н., Шарова Л.В. Интегральные неравенства и теория нелинейных колебаний. – М.:
Наука, 1976. – 150 с.