Monashova A.Z.

L.N.Gumilyov Eurasian National University, Astana

ABOUT ONE COMPACT PERTURBATION OF SECOND

 ORDER NON SELF ADJOINT OPERATOR 

In this paper it is studied the following operator

                                     ,  ,                          (1)

where , are complex-valued local-integrable functions in  .
We suppose that domain of operator  :   and the operator  is generated by the boundary condition .

We represent the function  in following way  where  and  are the real imaginary paints, respectively.

Further we also assume that the following conditions hold:

I.                    The function  is semi-bounded below function:  and   for almost all .

II.                For every  : .

III.             .

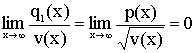Let  be the Friedrechs extension of the following semi-bounded below minimal operator

                               if ,

where  is the space of infinitely differentiable and finite functions in  .

Further by  we denote a unit ball in the space , namely

.

Let  be weighted Lebesque space with finite norm

, .

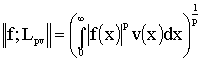For every  we define

                                    .

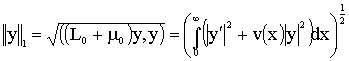Let  be the complement of  with respect to norm .

We consider Otelbaev function

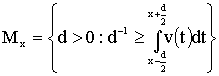                                ,                          (2)

Theorem 1. The following limitary equalities hold:

                                                , .                                       (3)

Proof. In (3) it is not obvious only limit equality when  tends to infinity. In the view of condition (II) for arbitrary   there exists  such that

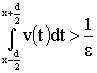
                                       (4)

If  for , then . Therefore  and  if . So it is proved that  if .

From theorem 1 it follows that the space  is compact embedded into space .

Corresponding theorem is proved in [2]. Here for the norm of embedding operator  the following estimates holds:

                                            (5)

The space  is the space of all absolutely continuous functions , which satisfy conditions: , .

From embedding  into  end estimate (5) is follows that for every  from

 

                                                            (6)

Let   be the complement of  with respect to norm (6).

 

Theorem 2. The operator , if  is continued to a compact operator .

Proof. It is sufficient to prove that for every  there exist number , not  depending on , such that

.                                             (7)

At first, from (7) we have the estimate of norm

.                                          (8)

Further for arbitrary sequences

,

Hence is the view of precompactness of  in  it follows (sequential) compactness of closure of  in .

Now we prove (7). At first, we note that

,                                    (9)

where , .

We choose  such that

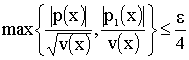 if .                                    (10)

We represent  as a sum

,                (11)

Where in the view of (10) the second summand

.                                    (12)

At first to estimate  we note that for  .

Therefore

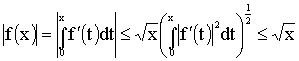 if .                    (13)

Let and a function  approximates in  with error . Then according to (13)

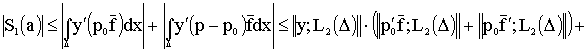
                                                                                              ,                      (14)

where  . Now we estimate norm .

We represent  as a sum

.               (15)

For  the following inequality hold

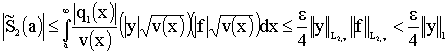.               (16)

For required estimate (13) we get

.                    (17)

According to estimates (9-17) we obtain inequality (7) with .

 

The author thanks Professor L.K.Kusainova for discussion of the presented results and for generous pieces of advice, which have improved the final version of this paper.

References

1.       Lions J.-L., Magenrs E. Non homogeneous boundary value problems and their application. Ì.:Mir.-1971

2.       Otelbaev Ì.Î., Mynbaev Ê.Ò. Weighted functional spaces and the spectrum of differential operator. Ì.:Nauka.-1988