Курлапов Л.И.

О ПРИМЕНЕНИИ УРАВНЕНИЯ ДВИЖЕНИЯ МЕЗОСКОПИЧЕСКИХ СИСТЕМ К МЕХАНИКЕ

СПЛОШНЫХ СРЕД

Мезоскопические системы состоят из мезоскопических частиц или содержат такие частицы в виде включений, и свойства таких систем определяются особенностями этих частиц. Особенность мезоскопических частиц связана с их малым размером и малой массой. Обычно их размеры составляют несколько нанометров, поэтому их называют наночастицами. Однако только размер частицы не является определяющим параметром. Главным свойством мезоскопических частиц является особенность их движения и взаимодействия, которые не соответствуют ни микрочастицам (атомам, молекулам и другим микрочастицам), ни макротелам, состоящим из огромного числа структурных элементов (микрочастиц).

Такое промежуточное положение мезоскопических частиц связано с главным природным явлением, которое отражается в аксиоме: все тела состоят из микрочастиц, участвующих в непрерывном тепловом движении. Именно это обстоятельство не позволяет применять ни физические и математические модели, разработанные для описания микрочастиц в виде модели материальной точки, ни модели, разработанные для описания абсолютно твёрдого макротела.

Исчезающе малые размеры микрочастиц (атомов, элементарных частиц) по сравнению с расстояниями между ними и возможность пренебречь их микроструктурой дали возможность моделировать их материальными точками и ввести для описания их движения такие понятия как радиус-вектор, скорость как производная от радиуса-вектора по времени, траектория движения в виде линии, сила, имеющая точку приложения и вызывающая ускорение материальной точки.

Огромная по сравнению с микрочастицей масса всего твердого тела позволяет пренебречь влиянием теплового движения микрочастиц и описывать движение и взаимодействия путём сосредоточения всей массы в центре масс тела и применения модели материальной точки к центру масс. Описание движения газа или жидкости основано на разбиении их на элементарные массы, которые также можно рассматривать как материальные точки. И в этом случае пренебрегается влиянием теплового хаотического движения отдельных микрочастиц (атомов, молекул) и взаимодействиями между элементарными массами.

Мезоскопическая частица занимает промежуточное положение. С одной стороны её масса сравнима с массой структурных элементов, из которых она состоит, поэтому их тепловое движение существенно сказывается на движении всей мезоскопической частицы. Хаотический характер теплового движения структурных элементов (микрочастиц) делает отчасти хаотическим и движением самой мезоскопической частицы, поэтому траектория движения расплывается в полосу, а движение становится не соответствующим закону движения материальной точки: закону Ньютона. Более того, мезоскопическая частица может участвовать в хаотическом движении и сталкиваться между собой и с другими частицами всей системы при этом она может рассыпаться или наоборот присоединять новые частицы. Такие явления наблюдаются в молекулярно-кластерной смеси газов, когда при определённых условиях в них существуют мезоскопические частицы в виде кластеров достаточно больших размеров. Такие кластеры могут навязывать газу свойства жидкости или твердого тела, но их столкновения не позволяют им образовать новую устойчивую фазу вещества [1, 2].

С другой стороны, несмотря на малые размеры, мезоскопическую частицу нельзя моделировать материальной точкой, так как она обладает внутренней структурой и, соответственно, внутренней энергией подобно макроскопической термодинамической системе. Конечный размер мезоскопической частицы говорит о том, что в разных её точках свойства могут различаться, причём из-за непрерывного теплового движения структурных элементов распределение структуры и массы по самой мезоскопической частицы изменяется со временем. Это приводит к неприменимости существующих моделей к описанию поведения мезоскопических систем.

Учесть особенности движения мезоскопических систем можно на основе необратимого по времени уравнения движения [3]:

. (1)

где

– плотность потока действия как характеристика взаимодействия протяжённых тел (двойная стрелка над символом говорит о том, что он обозначает тензор второго ранга),

– градиент необратимого потока за время действия,

– градиент теплового потока,

– диада из скоростей движения всей системы,

– плотность.

В этом уравнении взаимодействия описываются потоком действия, а отклик системы соответствующими потоками, которые в конкретном случае принимают определённый смысл. Применительно к механическому движению потоком действия является поверхностная плотность потока импульса, который для равновесия как изотропный тензор давления может быть представлен в виде произведения единичного тензора на скаляр – статическое давление. Такое описание в частности устраняет неопределённость введения давления. Широко распространённое определение давления (например, Википедия) как отношение проекции силы на нормаль к площадке к площади этой площадки неприемлемо, так как такая величина не образует поля, т.е. такое давление не является скаляром, поэтому к нему нельзя применять соответствующий математический аппарат. В то же время именно на этом основаны существующие методы вывода уравнений механики сплошных сред [4, 5].

В связи с новизной уравнения движения мезоскопических систем (1) возникает необходимость проверить его работоспособность путём сопоставления результатов с известными в тех условиях, когда это возможно проделать. В данной статье для этого приведён вывод уравнения движения сплошной среды в форме уравнения Эйлера и уравнения непрерывности. Для механических взаимодействий потоком действия будет поверхностная плотность потока импульса – тензор давления:

. (2)

При условии отсутствия внутренней энергии и теплового потока из этого уравнении можно получить уравнение Эйлера. Для данного случая уравнение (2) записывается так:

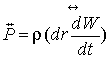, (3)

где двойной стрелкой над произведением 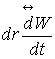обозначен (диадик) тензор второго ранга – диадное произведение вектора приращения радиуса-вектора на ускорение . Умножением с однократной сверткой обеих частей этого уравнения на вектор элементарной площадки с соответствующей нормалью, получим:

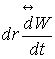() . (4)

Левая часть уравнения (4) преобразуются на основе теоремы Остроградского-Гаусса:

. (5)

Интеграл по объёму в правой части этого соотношения говорит о том, что на единицу объёма действует поток действия, равный вектору .

Правую часть уравнения движения (4)

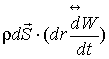(6)

можно привести к виду:

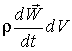==, (7)

из которого следует, что приращение импульса массы в единице объёма будет .

Приравнивая левую и правую части, отнесённые к единице объёма, получаем уравнение движения:

= . (8)

Видно, что полученное уравнение представляет собой уравнение Эйлера с учётом недиагональных компонентов тензора давления.

Таким образом, видно, что общее уравнение движения (1) в конкретном случае при определённых упрощающих допущениях даёт известное уравнение движения сплошной среды.

Для каждого внешнего воздействия в уравнении движения необходимо записывать соответствующий поток действия, поэтому для вывода уравнения непрерывности используется общее уравнение движения (1), (2), в котором потоком действия является градиент конвективного потока вещества, направленного против внешней нормали:

. (9)

После умножения (9) на единичный тензор с двойной свёрткой для данной задачи получим:

. (10)

Обычно уравнение непрерывности записывается для условия, когда отсутствует теплообмен, , и кинетическая энергия движения всей системы постоянна, . В таком случае (10) записывается в виде:

+=0. (11)

После преобразований это уравнение переходит в уравнение непрерывности:

+ =0 . (12)

Как видно из уравнения непрерывности (12), кроме обычных членов в нём присутствует градиент потока массы необратимой природы , что делает его необратимым. Это совпадает с уравнением, которое получается из кинетического уравнения с учётом различий конвективного и кондуктивного (необратимого) переноса [6, 7]. Такое же уравнение непрерывности выводится средствами механики неоднородных сплошных сред на основе модели доменов постоянной конфигурации, но переменного состава [6]. В такой модели сплошной среды возможно учитывать тепловое движение микрочастиц, и возникновение потоков необратимой природы объяснять переходами частиц из одного домена в соседний при их тепловом движении. Так как уравнение непрерывности используется при выводе и уравнения движения, и уравнения для энергии и энтропии, то влияние членов необратимой природы будут проявляются во всех уравнениях механики сплошных сред, а также в уравнении Лиувилля.

Из приведённых соотношений видно, что уравнение (1) даёт известные уравнения, причём при их выводе выявляются те допущения, при которых он справедлив с приемлемой точностью. В частности, видно, что статическое давление как скаляр можно получить из тензора давления только в условиях равновесия для изотропного тензора. Это приводит к необходимости определить условия применимости не только в виде условия локального термодинамического равновесии, но и условия локальной изотропности тензора давления. Через поток действия работа определяется как произведение потока на область действия. Для механического действия , что для локального равновесия и локально изотропного тензора это переходит в выражение термодинамики: =.

Как видно из уравнения непрерывности (12), в нём присутствует член, описывающий необратимый процесс переноса массы, а из (10) видно, что конвективный перенос и кондуктивный имеют разное происхождение, поэтому при интегрировании (12) для этих членов необходимо использовать различные граничные условия. Например, для диффузии в замкнутом приборе в виде двух сосудов, в которых находятся разные газы или поддерживается разная температура, и соединённых трубкой, на стенках трубки для скорости конвекции используются граничные условия прилипания, а для диффузионной скорости – диффузионная скорость, которая определяется по диффузионному потоку, . Видно, что диффузионная скорость в отличие от скорости механического перемещения не может быть определена как временная производная от радиуса-вектора, поэтому к ней нельзя применять правила нахождения суммы или разности, а сумма скорости обратимого движения и диффузионной скорости не может обладать никаким определённым свойством симметрии. Свойства диффузионной скорости присущи и другим скоростям, которые определяются по потоку необратимой природы, например, по тепловому потоку или по потоку энергии в других формах (например, в виде излучения).

Согласованность уравнения непрерывности с уравнением, полученным из кинетического уравнения позволяет применять формулы кинетической теории многокомпонентных систем для потоков и коэффициентов переноса и для описания мезоскопических систем. При этом необходимо учитывать, что в кинетическом уравнении в интеграле столкновений полевые частицы описываются локально-равновесными функциями. Такая особенность позволяет учитывать конечный размер частиц при выводе уравнений переноса из кинетического уравнения путём введения принципа заимствования частиц при перестановках их из элементарного объёма тестовых частиц в элементарный объём полевых частиц.

Как видно из приведённого в данной статье материала, широко применяемые соотношения механики сплошных сред представляют собой предельный случай уравнения движения мезоскопических систем, когда приемлемы условия локального термодинамического равновесия и локальной изотропности тензора давления. В общем случае особенности мезоскопических систем приводят к неприменимости существующих способов описания их поведения. В то же время именно такие системы представляют особый интерес не только в связи с выгодным их применением в новых технологиях, но и в связи с их негативным влиянием на окружающую природную среду. В связи с этим возникает необходимость в развитии мезоскопической физики, в которой должны разрабатываться физические и математические модели, способные отразить особенности мезоскопических систем и служить основой для предсказания их свойств.

Литература

1. Курлапов Л.И. Мезоскопия кластерных газов // ЖТФ. – 2005. – Т. 75, вып. 8. – С 136-139.

2. Курлапов Л.И.Расчет свойств газов на основе кластерной модели// ИФЖ. – 2003. – Т. 76 , №4. – С. 23-29.

3. www.rusnauka.com/72426.doc.htm ; www.rusnauka.com/44803.doc.htm.

4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. – Т.VI Гидродинамика. М.: Наука. 1986. –738 с.

5. Смирнов В.И. Курс высшей математики. Том 2. М.: Наука, 1974. – 656 с.

6. Курлапов Л.И. Физика кинетических явлений в газах. Монография. – Алматы, – 2001. 211 с. ISBN 9965-489-81-5.

7. Курлапов Л.И. Описание диффузии газов умеренной плотности на основе уравнения Больцмана-Лоренца-Энскога // ЖТФ. –1986. –Т.56, №2. – С.386-388.

The Summary

L.I. Kurlapov – lkurlapov@yandex.ru

ON APPLICATION OF THE EQUATION OF MOTION OF THE MESOSCOPICAL SYSTEMS TO THE MECHANICS OF CONTINUOUS MEDIA

From the irreversible equation of motion of mesoscopical systems [www.rusnauka.com/72426.doc.htm] the equation of motion of the continuous media and the equation of a continuity which contains a flow of mass of irreversible diffusion nature is received. It was possible only in a condition of thermodynamic equilibrium and a condition of local isotropic of pressure tensor that limits area of applicability of existing methods.