Гурвич Ю.А., Фулади Р., Ващёнок Ю.В.

Белорусский национальный технический университет

 АНАЛИЗ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК И ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ ДВУХШАРНИРНЫХ КАРДАННЫХ ПЕРЕДАЧ С ТРЕМЯ УГЛАМИ ИЗЛОМА

Связь между механизмами трансмиссий транспортных средств, например двигателя с коробкой  передач при ее раздельной установке, коробки передач с раздаточной коробкой и от нее к передним и задним ведущим мостам осуществляется с помощью карданных передач. В качестве примера рассмотрим подземный самосвал БелАЗ-75800 (Рисунок1) и его кинематическую схему (Рисунок2).

62

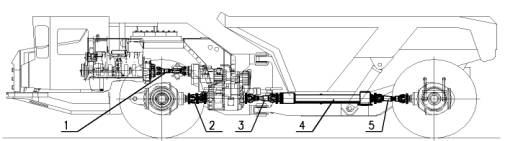
Рисунок 1 – Подземный самосвал БелАЗ-75800: 1- карданный вал коробки передач; 2- карданный вал переднего моста; 3- карданный вал промежуточной опоры (промопоры;  4 – промопора; 5- карданный вал заднего моста.

71

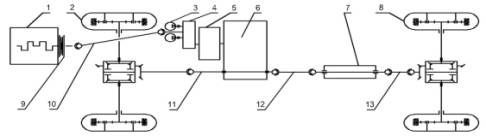
Рисунок 2 – Кинематическая схема трансмиссии подземного  самосвала БелАЗ-75800: 1- ДВС; 2- мост передний; 3- насосы рулевого управления; 4- передача согласующая;  5- гидротрансформатор; 6- коробка передач;  7-промопора; 8- мост задний; 9- муфта демпферная; 10- карданный вал коробки передач; 11- карданный вал переднего моста;  12- карданный вал промопоры; 13- карданный вал заднего моста.

 Карданная передача состоит из одного или нескольких карданных шарниров (рисунок 3).

73

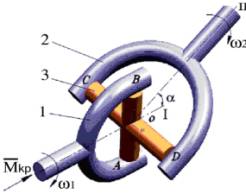
Рисунок 3 – Кинематическая схема карданного шарнира: 1, 2 – вилки; 3 – крестовина; I – ось вращения вилки I;  II – ось вращения вилки 2;α -  угол между осями I и II;  III – новое положение оси вращения вилки 2 при переменном угле α; и - угловые скорости ведущего и  ведомого валов;

На рис. 4 приведена схема карданной передачи с двумя карданами. При различных углах наклона карданной передачи изменяется длина шлицевого соединения s, вследствие изменения длины . В результате изменения длины  шлицевого соединения, являющиеся непрерывной функцией времени, изменяется жесткость системы. Подчеркнём, что для иллюстрации работы шлицевого соединения на рисунке 4 показаны три дискретных положения конца шлицевого вала: крайнее левое –  среднее – ; крайнее правое – ; s= ;

 Рассмотрим случай, когда вилка 2 сдвинута относительно вилки , повернутой относительно вала II на угол θ, по направлению вращения на угол , вследствие чего вал III смещен на некоторый угол  от первоначального положения. Пусть вал I повернулся на некоторый угол . На такой же угол повернулась от горизонтальной плоскости вилка 1. Вал II повернется на угол  Таким образом для углов и имеем:

.                                                  (1)

 

А-А

                           y                                          y                                                 y

 

 

 


                                                                 

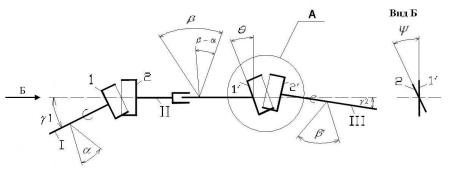
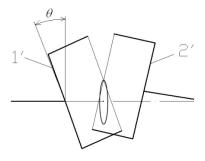
Рисунок 4 - Схема карданной передачи с двумя шарнирами и обозначением углов:  - угол поворота вала I;  - угол поворота вала III;  - угол излома вала I;  - угол излома вала III;  - угол между вилками 2 и 1’, расположенными на валу II

Если бы обе вилки карданов на валу II вначале движения лежали в одной горизонтальной плоскости, то для определения соотношения между углами  и  можно было бы применить уравнение (1), предположив, что вся система повернулась на угол, равный , т. е. в этом случае получаем следующее соотношение, между углами  и

 или .

Ранее было принято, что вилка  смещена по отношению к вилке 2 на угол , а по отношению к вилке 1 на угол . Поэтому  получаем такое соотношение между углами и:

 или

                            .                                      (2)

Решая это уравнение относительно , получим:

;

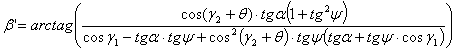, (3)

где θ – угол излома между вилкой 1’ и валом II.

Получим формулы для определения угловой скорости ω3 и углового ускорения ε3 поворота ведомого вала III.

Из соотношения (3) видно, что угол  является функцией двух переменных  и . Следовательно, полная производная по времени от  будет представлять собой сумму двух слагаемых:

.                                                    (4)

Выражение (4) перепишем в виде:

.                                                (5)

Определим угловое ускорение ведомого вала , взяв полную производную по времени от левой и правой частей выражения (5):

,            (6)

где , , - угловые ускорения валов I и III соответственно.

          Отметим, что впервые получено значение углового ускорения  в функции трёх углов:  , , θ.

          В динамике колесо, сидящее на валу III, получит дополнительный момент, равный произведению момента инерции колеса с карданной передачей Iy на угловое ускорение , что вызовет дополнительное осциллирующее вращение колеса вокруг его оси. Таким образом, колесо получает три движения: первое – вращение колеса вокруг собственной оси; второе – поступательное движение колеса, которое вместе с вращением колеса образует плоско-параллельное движение (это происходит под действием Мкр двигателя); третье – осциллирующее движение колеса под действием дополнительного момента  М= ± Iy · , который вызовет негативные явления, заключающиеся в дополнительном износе шин и поломке игольчатых подшипников и т.д.

         Рассмотрим параметрические колебания карданной передачи. Составим уравнение свободных колебаний системы, считая, что они происходят в плоскости чертежа (Рисунок 4).

 Если в текущий момент време­ни t перемещение массы составляет у, то восстанавливающая сила упругости карданного вала равна – су. Тогда уравнение движе­ния массы имеет вид

где с — коэффициент жесткости системы.

Коэффициент жесткости с можно определить по известной формуле

Здесь предполагается, что кардан имеет постоянное поперечное сечение с осевым момен­том инерции J; через Е обозначен модуль упругости материала кардана. Таким образом, дифференциальное уравнение (7) принимает вид

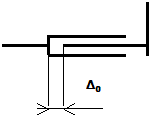
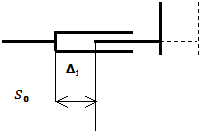
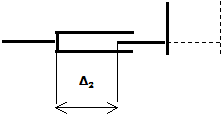
Допустим теперь, что вал скользит во втулке, следуя закону

т. е. вал совершает гармонические колебания с амплитудой А и круговой частотой здесь s0 — среднее расстояние от шарнира до вала. В этом случае коэффициент жесткости оказывается функцией времени:

и дифференциальное уравнение (4) становится уравнением с переменными коэффициентами – уравнением типа Матье:

Колебания теперь уже нельзя называть свободными, так как они происходят на заданном во времени внешнем воздействии в виде периодического изменения жесткости системы. С другой стороны, их нельзя назвать и вынужденными, так как внешнее воздействие не представляет собой возмущающей силы, а входит в левую часть уравнения движения. Колебания подобных систем, происходящие при заданном изменении параметров системы, называются параметрически возбуждаемыми, которые описываются уравнением Матье. Параметрические колебания возникают при наличии какого-либо переменного параметра, создающего эффект, аналогичный действию переменной силы. Обычно таким параметром является переменная жесткость детали или узла. При этом возникает так называемый параметрический резонанс.

Возможность передачи мощности от двигателя к механизмам трансмиссии, удаленных друг от друга и расположенных в разных плоскостях, изменяющих свое первоначальное положение в процессе движения машины, выгодно отличает карданные передачи. Однако, помимо достоинств, карданная передача обладает существенным недостатком, заключающимся в неравномерности вращения выходного вала, возникающей из-за угла излома и двух других углов. Эта неравномерность негативно сказывается на работе элементов карданных передач и механизмов трансмиссии.