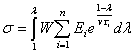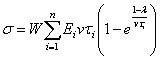Сеничев В.Ю.

Институт технической химии УрО РАН, г.Пермь, Россия

Особенности описания деформационного поведения сшитых эластомеров в условиях растяжения с постоянной скоростью

Деформационное поведение сшитых эластомеров в условиях деформирования с конечной скоростью может быть описано только с учетом релаксационных характеристик рассматриваемых объектов. Однако принятие в учет только релаксационной составляющей отклика полимерного объекта на механические воздействия не позволяет учитывать те особенности влияния на эластичность указанного объекта степени деформирования, которые связаны со строением и свойством химической сетки в сшитом эластомере. Кроме того известно, что скорость деформирования может влиять на процессы ориентации жестких блоков в эластомерах со сложной фазовой структурой [1,2], однозначно сказываясь на уровне механических свойств.

Целью настоящей работы являлось изучение возможности описания зависимость напряжение-деформация в условиях деформирования с конечной скоростью с использованием положений теории высокоэластичности с учетом релаксационной природы реальных эластомеров.

В качестве объектов экспериментов использовали простые полиэфируретаны серии BBL, которые были изготовлены на основе олиготетраметиленгликоля (полифурит) с молекулярной массой 1000, дифенилметандиизоцианата(МДИ), бутандиола-1,4 и триметилолпропана (Табл.1). Предварительно часть полифурита была использована для получения псевдофорполимера СКУ-МB-4. При получении данного псевдофорполимера мольное соотношение полифурит: МДИ составляло 1:4. Готовый псевдофорполимер отверждали смесью бутандиола и триметилолпропана. Режимы синтеза образцов соответствовали работе [3].

Наиболее просто релаксационная сторона природы эластомеров может быть учтена с использованием подхода линейной вязкоэластичности, наиболее подходящего для сшитых эластомеров, т.к. это предполагает наличие постоянного остаточного напряжения в релаксационных экспериментах [4,5]. В рамках данного подхода зависимость напряжения от деформации для простого растяжения с постоянной скоростью для системы, состоящей из n релаксационных элементов, может быть записана с помощью следующего выражения:

(1)

где W- функция трансформации, λ – степень деформации, v – скорость растяжения, E_i , τ_i – релаксационные параметры, имеющие размерность напряжения и времени соответственно. Под функцией W можно понимать изменение эластичности релаксационных элементов по мере деформирования, не связанное с релаксационными процессами. Ее можно рассчитать исходя из применяемой модели высокоэластичности по выражению:

(2)

Ранее было установлено, что при и выражение (1) может быть записано в упрощенной форме [4]:

(3)

Ранее авторы разработали обобщенный подход к описанию деформационного поведения сшитых эластомеров в равновесных условиях деформирования [3,6]. Указанный подход основан на использовании МСС-модели Эрмана-Моннери, которая удачно описывает деформирование сшитых эластомеров на начальной стадии растяжения [7], и концепции конечной растяжимости полимерных цепей [8,9], которая позволяет учесть упрочнение полимерных цепей при высоких степенях растяжения.

Рассмотрим выражение (3) исходя из MCC-модели Эрмана-Моннери. Величину функции трансформации для этой модели можно рассчитать по следующим выражениям [4]:

при	(4)
при	(5)

где b,d – параметры сетки. Обычно , .

Поскольку упомянутая модель не учитывает фактор конечности растяжимости полимерной цепи, необходимо было провести коррекцию выражений для функции трансформации с учетом указанного фактора. Для этого можно использовать выражение, выведенное ранее в рамках указанного обобщенного подхода для зависимости напряжения от деформации сшитых эластомеров с трехфункциональными узлами при простом растяжении [3]:

(6)

Где f – вспомогательная функция, .

Дифференцирование уравнения (6) позволяет получить следующее выражение для функции трансформации:

(7)

где a- коэффициент нерастяжимости цепи, γ_s - поправочный структурный параметр. Для одиночной полимерной цепи справедливо следующее выражение , где λ_max- максимально возможная для данной плотности сетки степень растяжения. При больших деформациях энтропия уменьшается и когда полимерная цепь полностью вытянута, свободных конформаций, которые бы могла принимать полимерная цепь, уже не остается. В этих условиях, таким образом, конформации цепей не подчиняются распределению Гаусса, и простая гауссова статистика теории высокоэластичности неприемлема.

Адекватность использования выражения (7) необходимо было рассмотреть в области реальных параметров конечной растяжимости исследованных эластомеров. Для этого были выбраны следующие области величин параметров a и g_s: и соответственно, находящиеся в области реальных значений, полученных ранее [3,6].

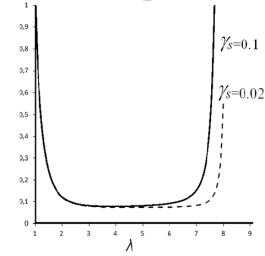
Для оценки роли параметра g_s выберем значение a=0.12, при котором действие фактора конечной растяжимости должно быть более заметным (это соответствует разрывным деформациям 733%). На рис. 1 нанесены кривые зависимостей W=f(λ) при двух крайних значениях параметра g_s. Как наглядно видно, величина параметра g_s не влияет значительно на форму графика функции W=f(λ), являясь важным корректирующим фактором только на конечной стадии растяжения.

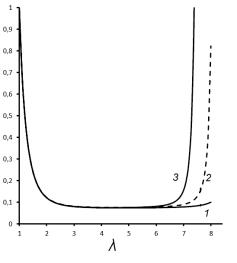
Рис.1 График зависимости (7) при значении a=0.12 и двух значениях параметра gs.	Рис.2 График зависимости (7) при значении gs =0.03 и трех значениях параметра a: 0.11(кривая 1), 0.12(кривая 2), 0.13(кривая 3).

Значительно сильнее на форму кривой, соответствующей выражению (7) влияет величина параметра a. Это влияние продемонстрировано на рис.2. Как видно из графика, изменение данной величины в диапазоне вызывает резкий рост величины функции W в области больших степеней деформации.

Очевидно, что использование выражения (7) для расчета функции W и последующее использование в уравнениях (1) или (3) является неправомерным относительно релаксационных элементов со временем релаксации в диапазоне менее 10⁴с, т.к. при растяжении быстро релаксирующих полимерных цепей понятие конечной степени растяжения теряет физический смысл. Как будет показано ниже (рис.6), использование выражения (7) для учета вкладов релаксационных элементов в напряжение приводит к получению результатов, заведомо завышенных по величине напряжения.

В силу этого использование выражений (4,5) для сшитых эластомеров остается правомерным даже с учетом фактора конечной растяжимости, за исключением нерелаксирующей части напряжения, зависимость которой от степени деформации передается уравнением (6).

С учетом вышеизложенного, обобщенное выражение для зависимости напряжения от деформации должно включать два вклада в напряжение:

(8)

Где первая составляющая σ₁ рассчитывается по выражению (1) или (3), а вторая σ₂ по выражению (6).

Углубленная экспериментальная проверка выражения (8) была проведена для образцов BBL при трех скоростях растяжения. Релаксационные параметры определялись методом Бартенева-Лялиной [10], см. Табл.2.

Расчеты показали, что параметры g_s и a, связанные с конечной растяжимостью полимерной цепи, при изменении скорости деформирования в исследованном диапазоне изменялись незначительно, что дает возможность использовать при расчете зависимостей напряжения от деформации при разных скоростях деформирования постоянные значения данных параметров.

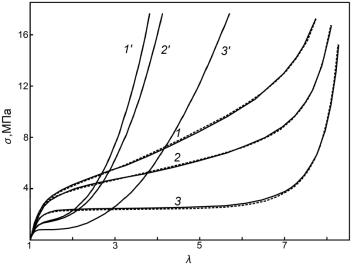
На рис.3-6 показано соответствие экспериментальных кривых для образцов серии BBL для трех скоростей растяжения, и расчетных, полученных при использовании для уравнения (1) выражения (8). При этом выражения (4,5) используются для расчета релаксирующей части напряжения σ₁ , а выражение (7) для нерелаксирующей σ_2. В том случае, если применять для расчета функции W обоих составляющих только выражение (7), расхождение расчетных кривых и экспериментальных становится исключительно большим (рис.6).

Выводы

Исследовано деформационное поведение серии сшитых полиэфируретановых эластомеров. Установлено, что зависимость напряжения от степени деформации для простого растяжения при постоянной скорости может быть описана с использованием линейной модели вязкоупругости и обобщенной модели высокоэластичности, разработанной ранее для равновесных процессов.

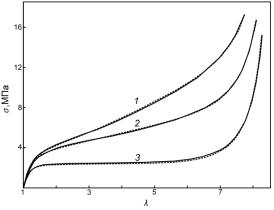
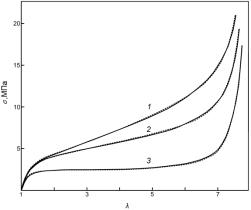
Рис.3 Зависимость напряжения от деформации для образцов BBL-1 при трех скоростях растяжения: 0.56 с^-1 (1), 0.056 с^-1 (2) и 0.0028 с^-1 (3). Сплошные линии – эксперимент, пунктир – расчет по уравнению (8) с учетом выражений (4,5,7).	Рис.4 Зависимость напряжения от деформации для образцов BBL-2 при трех скоростях растяжения: 0.56 с^-1 (1), 0.056 с^-1 (2) и 0.0028 с^-1 (3). Сплошные линии – эксперимент, пунктир – расчет по уравнению (8) с учетом выражений (4,5,7).
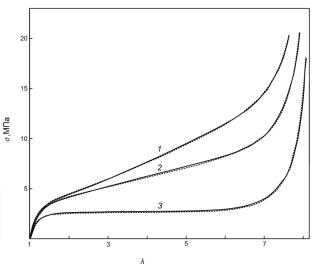
Рис.5 Зависимость напряжения от деформации для образцов BBL-3 при трех скоростях растяжения: 0.56 с^-1 (1), 0.056 с^-1 (2) и 0.00277 с^-1 (3). Сплошные линии – эксперимент, пунктир – расчет по уравнению (8) с учетом выражений (4,5,7).	Рис.6 Зависимость напряжения от деформации для образцов BBL-1 при трех скоростях растяжения: 0.56 с^-1 (1), 0.056 с^-1 (2) и 0.00277 с^-1 (3). Сплошные линии – эксперимент, пунктир – расчет по уравнению (1) с учетом выражений (3,4). Линии 1’, 2’, 3’ –расчет по уравнению (8) с учетом расчета функции W только согласно выражению (7).

Таблица 1. Состав полиуретановых образцов серии BBL (в мольных долях)

Образец	СКУ-МB-4	Полифурит (ММ 1000)	Этриол	Бутандиол	CHS
BBL-1	1.08	0.15	0.03	0.85	0,475
BBL-2	1.08	0.1	0.03	0.9	0,500
BBL-3	1.08	0.05	0.03	0.95	0,532
BBL-4	1.08	0	0.03	1	0,559

Таблица 2. Параметры уравнения (2) для эластомеров серии BBL

Образец	Релакса-ционный элемент	τi, c	Ei, МПа	a			gs
				Скорость, с^-1			Скорость, с^-1
				0.0028	0.056	0.56	0.0028	0.056	0.56
BBL-1	1		39.1	0.11	0.11	0.10	0.05	0.052	0.051
	2	1040	4.7
	3	120	7.2
BBL -2	1		52.8	0.12	0.12	0.12	0.04	0.04	0.042
	2	1030	4.9
	3	52	7.6
BBL -3	1		83.6	0. 11	0.10	0.11	0.030	0.032	0.031
	2	1120	5.3
	3	54	7.7

Литература

1. Tereshatov V.V., Makarova M.A., Senichev V.Yu., Slobodinyuk A.I. Interrelation between ultimate mechanical properties of variously structured polyurethanes and poly(urethane urea)s and stretching rate thereof // Coll. Polym. Sci. 2012. V.7. P.641-651.

2. Tereshatov V.V., Makarova M.A., Senichev V.Yu., Volkova E.R., Vnutskikh Zh.A., Slobodinyuk A.I. The role of the soft phase in the hardening effect and the rate dependence of the ultimate physico-mechanical properties of urethane-containing segmented elastomers// Coll. Polym. Sci.-2015. V.293. P.153-164.

3. Tereshatov V.V., Senichev V.Yu. Stress–Strain Dependence of Cross-Linked Single-Phase Polyether Urethane // Journal of Macromolecular Science, Part B: Physics. 2014. V.53. P.575–587.

4. Tereshatov V.V., Senichev V.Yu. Stress-strain behavior of cross-linked polybutadiene urethanes // Polym. Sci. 1995. V.37A. P.702-705.

5. Tereshatov V.V., Senichev V.Yu. The effect of low-molecular liquids on physical network and viscoelastic properties of cross-linked amorphous polydieneurethanes // Polym. Sci. 1995. V.37A. P.1164-1171.

6. Tereshatov V.V., Senichev V.Yu. Stress–Strain Dependence of Segmented Polyurethanes and Polyurethane Ureas // Journal of Macromolecular Science, Part B: Physics. 2015. V.54. P.365–380.

7. Erman B., Monnerie L. Theory of elasticity of amorphous networks: effect of constraints along chains // Macromolecules. 1989. V. 22. P.3342-3348.

8. Horgan C.O., Saccomandi G. Finite thermoelasticity with limiting chain extensibility // Journal of the Mechanics and Physics of Solids-2003. V. 51. P.1127 – 1146.

9. Zrinyi M., Kilian H.-G., Horkay E. On the decisive role of finite chain extensibility and global interactions in networks // Coll. Polym. Sci. 1989. V.267. P.311-322.

10. Бартенев Г.М., Лялина Н.М. Определение релаксационных параметров полимеров расчетно-графическим методом // Высокомолекулярные соединения. Сер.А. 1970. Т.12. №2. С. 368-384.