Е.Т.Божанов, Г.А. Тулешева,  К.Д.Мурзасаимова

 

Казахский национальный исследовательский технический университет имени К.И.Сатпаева,

Казахстан, Алматы

nurai_mak@mail.ru

 

Расчет одной математической модели трубчатой конструкции и днища, выполненных из различных материалов

 

УДК 532:536.24;533.9

            Постановка задачи.

1.1 Рассмотрим трубчатую тонкостенную конструкцию с переменными параметрами. Торцы каркаса и днища выполнены из различных материалов с приведенным модулем разномодульных соединений. При этом внецентренно сжатый стержень при сжимающей нагрузке и ударного импульса превращается в податливую нить за пределом теории упругости. Для определения несущей способности такой конструкции допускаемые значения деформации задаются в граничных условиях на стыке и под нагрузкой. Расход материала днища определяется , где -диаметр отпечатки контактного                воздействия, -плотность овального очертания поперечного сечения конструкции длиной-  . 

            Тогда варьируя нагрузку контактного воздействия под нагрузкой и  теоретическую схему связи между внешними и внутренними силами в рамках принципов механики тонкостенной конструкции [1]-[4] математическую модель запишем в виде:

                                                           (1)

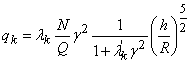где    ,                                                                        (2)

- коэффициент формы поперечного сечения отпечатки,   -  коэффициент континуума Коссера,  - анизотропные характеристики материала, - число полуволн в продольном направлении, - коэффициент формы нелинейных деформационных процессов, -толщина, -наименьший радиус отпечатки контактного воздействия.

            Общее решение дифференциального уравнения (1) есть [5]:

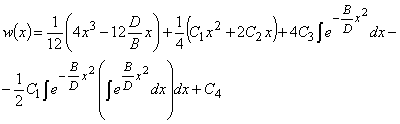                                             (3)

В частности в первом приближении:

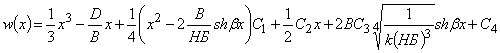              (4)

.

Граничные условия на торцах и под нагрузкой:

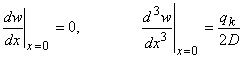                                                  (5)

                                             (6)

            Подставляя (4) в (5) и (6) определим произвольные постоянные С1, С2, С3, С4. Затем их значения подставляя в общее решение (4) получим:

 

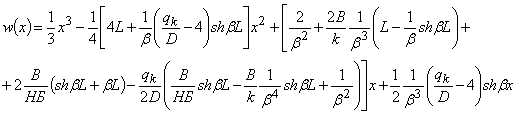           (7)

Здесь

                                                              (8)

 

1.2 Расчет площадки контакта на стыке каркаса и днища трубчатой конструкции под действием сосредоточенной сдвигающей силой.

            В частности если комплексная податливость материала конструкции не влияет на коэффициент потери массы континуума Коссера днища, то математическая модель (1) будет:

 

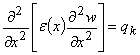,                                                        (9)

При следующих граничных условиях:

С1=С2=0;                                       (10)

Частное решение которого есть:

                                                    (11)

            Формула (11) вычислена с применением прикладных программных продуктов при следующих заданиях:

Задание 1. Построить график функции в долях  при

  т.е.

                                                    (12)

Задание 2. Построить график функции, когда материал днища есть   при

     т.е.

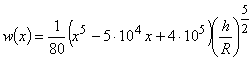                                                    (13)

Задание 3. Построить график функции, когда материал днища есть  каст-В, ПН-3  при

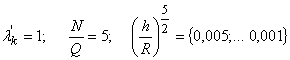       т.е.

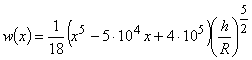                                                    (14)

 

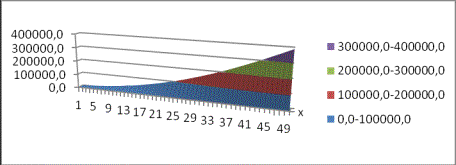
График 1. Расчет площадки контакта на стыке каркаса и днища, когда

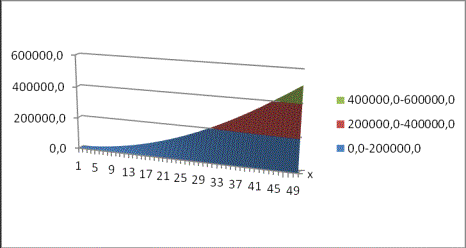
График 2. Расчет площадки контакта на стыке каркаса и днища, когда

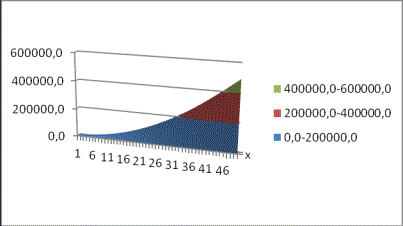
График 3. Расчет площадки контакта на стыке каркаса и днища, когда 

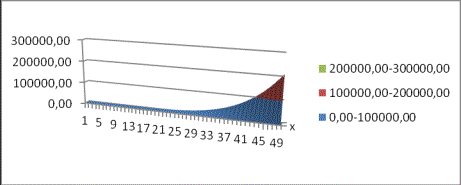
График 4. Расчет площадки контакта на стыке каркаса и днища в долях

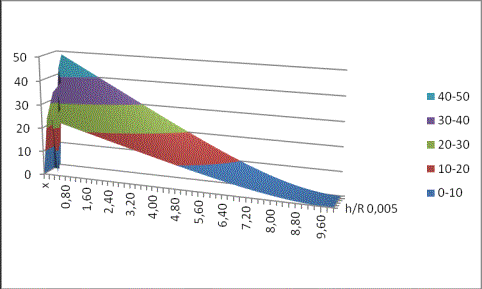
График 5. Расчет площадки контакта на стыке каркаса и днища из

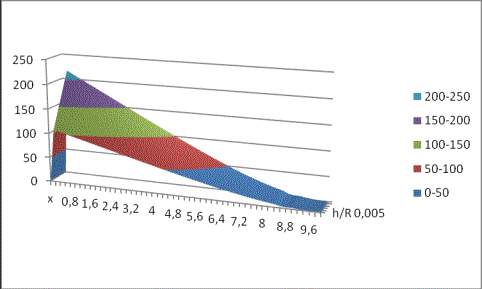
График 6. Расчет площадки контакта на стыке, когда материал днища есть  Аст-В, ПН-3

 

Выводы:

Результаты счета, приведенные в графиках 1-3, показывают, что параметры  разупрочняющее воздействие в упруго-вязкой области оказывают существенное влияние и на величину смещений контура на стыке.

Как видно из графиков 4-6 большему значению сосредоточенной сдвигающей силы соответствует меньшее смещение контура площадки контакта на стыке каркаса и днища, тем самым вновь подтверждена существенная роль влияния прочнистных  и деформационных свойств материала днища типа континуума Коссера.

Зависимость смещений контура площадки контакта от комплексной податливости материала конструкции зависит от коэффициента потери массы днища с учетом его разупрочняющего воздействия и от действии сдвигающего импульса.

Как показывает расчет тонкостенной конструкций наибольший расход материала спаики потребуется для случая изменения твердости матрицы материала по Бринеллю диаметра отпечатки и ударного импульса.

 

 

Литература.

БожановЕ.Т., Ержанов Ж.С. Исследование проблем устойчивости упругих тел, гибких пластин и оболочек и их приложения//  Алматы:Қазақстан жоғары мектебі. 2001. С.300.

Божанов Е.Т., Отарбаев Ж.О., Буганова С.Н. Математическое моделирование геомеханических процессов// Алматы: 2015. С.145.

Е.Т.Божанов, Г.А. Тулешева, К.Д.Мурзасаимова, К. Хойлан. Об одной модели Б-6 относительного прогиба трубчатой конструкции из композита// ІІ Международная научно-практической конференция «Информационные и телекоммуникационные технологии: образование, наука, практика».  Алматы.2015. I том. С.143-147.

Г.А. Тулешева, Е.Т.Божанов, К.Д.Мурзасаимова, А. Надирбеков. Об одной модели Б-6 трубчатой конструкции из композиции эластомеров// ІІ Международная научно-практической конференция «Информационные и телекоммуникационные технологии: образование, наука, практика».  Алматы.2015. I том. С.275-278.

Дадаева А.Н., Божанов Е.Т., Акимжанова Ш.А., Курмангали А. Об одной математической модели технологии усадки порошкового материала при неподвижной матрице // ІІ Международная научно-практической конференция «Информационные и телекоммуникационные технологии: образование, наука, практика».  Алматы.2015. I том. С.158-163.

.