HOVHANNISYAN T.N.

STABILITY OF MULTIVARIABLE L1 ADAPTIVE CONTROL SYSTEMS

The paper examines the stability of MIMO (i.e. Multiple-Input Multiple-Output) adaptive control systems based on the properties of positive real transfer matrices. Such systems are stable for large values of the adaptation gain, even in the case of systems with right half plane zeros.

Keywords: multivariable (MIMO) control system, adaptive control, reference model, positive real system, stability.

adaptive control was developed to address some of the drawbacks evident in Model Reference Adaptive Control (MRAC), as a loss of robustness in the presence of fast adaptation [3,4].

As a basic model of linear -dimensional, i.e. having inputs and outputs, MIMO systems with constant parameters let us consider the system that can be expressed in the following standard state-space form:

(1)

where is an -dimensional state vector; and are -dimensional vectors of inputs and outputs; are constant matrices of appropriate sizes. We will assume that system completely controllable and observable, strictly stable, and, maybe, with Right Half Plane (RHP) zeros.

The MIMO system (1) can also be described in the operator form by the scalar strictly proper rational matrix in complex variable s.

Generally, the transfer matrix is connected with the matrices in (1) by the formula [5]

, (2)

where is an identity matrix.

We will adhere to the architecture with state predictor and low-pass matrix filter presented in [2]. Let an -dimensional strictly stable multivariable system be described in state-space by the following equations:

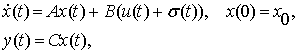(3)

where is an -dimensional time-dependent vector of unknown externally bounded () disturbances that should be rejected by adaptive control, and all other matrices and vectors have the dimensions as in (1).

The state predictor has the same structure as the system in (3). The only difference is that the unknown disturbance vector is replaced by its estimate .

The process is regulated by the following adaptation law [2]

, (4)

where is the prediction error, is the solution of the Lyapunov equation

(5)

for an arbitrary symmetric positive definite function (), and the positive scalar is called the adaptation gain [2].

The control signal of the system is given in operator form as

, (6)

where is an -dimensional reference signal, is an static (gain) matrix, and is the transfer matrix of a low-pass filter.

In the Fig. 1, it is shown general block diagram of the multivariable adaptive control system (4) with integral feedback and disturbance rejection law [2].

Fig. 1. Block diagram of the adaptive multivariable system with the state

predictor and the adaptive disturbance rejection law

The architecture of the discussed adaptive MIMO control system represents a linear multivariable system with integral feedback and therefore can be investigated by the methods and approaches of linear multivariable feedback control [5,6].

Based on the block diagram in Figure 1, it is easy to derive the following matrix equations of the adaptive system with the state predictor:

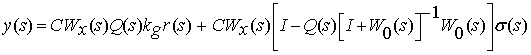, (7)

where

; . (8)

From the matrix equation (8) can be seen that the output signal of the system consists of two components, where the first one describes the system behavior with respect to the reference signal while the other is generated by the disturbance .

Let us proceed to the stability analysis of the adaptive system in Figure 1. From the first summand of the matrix equation (7), it is evident that it represents a stable open-loop MIMO system, which does not depend on the adaptation gain . Therefore, no problem with stability can arise here. The second part of the equation contains a negative feedback loop system, where transfer matrix in (8) can be written in the state-space form as

(9)

where

. (10)

Taking into account the form of the matrix (10) and recalling the Kalman-Yakubovich lemma [2-4, 7], we come to a conclusion that belongs to the so-called Positive Real (PR) transfer matrices for which the Hermitian matrix is positive semi-definite for all real , for which is not a pole of any element of . As shown in [6], the condition implies that all his scalar Characteristic Transfer Functions (CTFs) are also Positive Real, that is for all real . This means that all are strictly stable and minimum-phase, have relative degree 0 or 1, and the Nyquist plots of lie entirely in the right half complex plane or, which is the same, the phases of are always less or equal to .

The same is true for CTFs of the transfer matrix (8). They have relative degree 1 or 2 and are minimum-phase, even if the initial system has RHP transmission zeros, which implies that the Nyquist plots of cannot encircle the critical point , irrespectively of the value of the gain .

Summarizing, it is shown that the adaptive system in Figure 1 is stable for any strictly stable transfer matrix and any value of the adaptation gain . That feature ensues from the fact that the transfer matrix (8) always belongs to the class of Positive Real matrices.

Example. The results of simulation of the two-dimensional adaptive system with the help of Simulink for , sinusoidal disturbances with unit amplitudes in both channels and the period , where the oscillations in the second channel are shifted by degrees, and two different values of the adaptation gain ( and ) , are shown in Figure 2. The increase in brings to smaller deviations of from zero, i.e. to the higher performance of the adaptive system (the absolute maximum deviation of the output signals for is more than 20 times as small as for ). The further increase in will result in smaller errors tending to zero as .

Fig 2. Simulation results: (a),(b) ; (c),(d) .

References

1. T. Hovanissyan, N. Vardanyan, E. Kharisov, O. Gasparyan, Hovakimyan N. On Application of L1 Adaptive Control to Multivariable Control Systems. Part I. General-Type Multivariable Systems // Известия НАН и ГИУА. Сер. ТН. – 2014. – Т.67, №4. – С. 434-445.

2. Hovakimyan N. and Cao. C. Adaptive Control Theory - Guaranteed Robustness with Fast Adaptation. - SIAM, Philadelfia, 2010. – 340 p.

3. Astrom K. and Wittenmark B. Adaptive Control. - Addison-Wesley Longman Publishing Co., Inc., Boston, MA, 1994. -575 p.

4. Ioannou P. and Sun J. Robust Adaptive Control. - Prentice Hall, 1996. – 834 p.

5. Skogestad S. and Postlethwaite I. Multivariable Feedback Control. Analysis and Design. -John Wiley and Sons Ltd., Chichester, Sussex, UK, 2005. - 595 p.

6. Gasparyan O. N. Linear and Nonlinear Multivariable Feedback Control: A Classical Approach. - John Wiley & Sons, UK, 2008. - 354 p.

7. Slotine J.-J. E. and Li W. Applied Nonlinear Control. - Prentice Hall, Englewood Cliffs, USA, 1991. - 476 p.