Технические науки/3.Отраслевое машиностроение

Д.т.н. Касьянов В.Е., Теплякова С.В.

Ростовский государственный строительный университет, Россия

Определение параметров выборочного и совокупности конечного объема распределений Вейбулла для гарантии безотказности деталей машин

Опыт сбора информации о надежности машин, в том числе и одноковшовых экскаваторов [1], базировался на получении данных об отказах, ремонтах и техническом обслуживании при наблюдениях за выборками машин в количестве n=10-100.

Во многих учебниках по теории вероятностей и математической статистике рассматриваются генеральные совокупности бесконечного объема. Вместе с тем известно, что в эксплуатации находятся тысячи однотипных машин, образуя совокупность конечного объема. Лишь в некоторых литературных источниках рассматриваются такие совокупности и выборки из них [2-4].

Сбор информации о надежности показывал, что отказы возникают не только от машин, входящих в выборку, а от совокупности однотипных машин, что и у выборки.

Параметры А_с и В_с совокупности находятся с помощью рекомендаций ГОСТ 11.008-75 [5], с использованием вероятностной сетки закона Вейбулла. Предположили, что при нанесении экспериментальных выборочных точек на вероятностную сетку с последующей аппроксимацией их прямой линией для получения прямой распределения совокупности достаточно продлить выборочную прямую до первого значения вариационного ряда совокупности. При этом вероятность первого (минимального) значения вариационного ряда составит Q=1/N_c, N_c – объем конечной совокупности.

Сделанное предположение по определению параметров А_с и В_с проверено путем сравнения моделированных значений по параметрам А_с и В_с с экспериментальными выборочными данными. В результате сравнения ошибки составили δ=0,06-2,02%.

Параметры а, b для распределения Вейбулла по выборочным данным найдены из графика 1 [6].

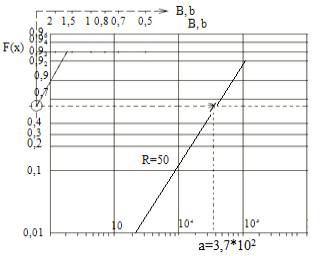
Рис. 1. Графический метод определения параметров выборочного распределения Вейбулла

Довольно низкий процент расхождения δ=0,06-2,02% позволил принять численные значения параметров выборки a=А_с и b=В_с. Третий параметр С_с-сдвига совокупности распределения Вейбулла получается экстраполяцией левой ветви распределения до пересечения с осью абсцисс. При этом получаемый сдвиг распределения оказывается меньше первого (минимального) значения вариационного ряда совокупности, то есть этот сдвиг С_с попадает в зону отсутствия отказов, поэтому вместо сдвига С_с можно использовать первое значение вариационного ряда совокупности 1 [7].

Рис. 2. Распределения ресурсов деталей: 1-по выборочным данным; 2-по данным совокупности конечного объема

Известно, что рассеивание выборки меньше, чем рассеивание совокупности, поэтому в соответствии с этими выводами и рис.2 левая ветвь совокупности длиннее, чем у выборки и рассеивание (размах) больше, чем у выборки, то есть отказы совокупности начинаются раньше, чем у выборки.

Для обеспечения высокой безотказности и даже абсолютной безотказности необходимо иметь гарантийный запас по ресурсу, превышающий заданный ресурс на 15-30%, а в некоторых случаях и больше. Для этого выполнено моделирование, то есть нахождение минимального (первого) значения вариационного ряда. В качестве примеров принято несколько значений выборочных размахов R=1,25; R=20; R=50 (рис.3-5), применительно для какой-либо детали машины.

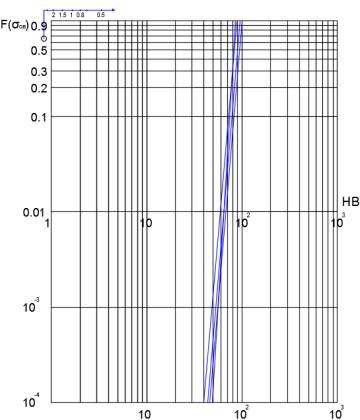
Рис.3. Распределения выборок твердости стали и их генеральных совокупностей с размахом R=1,25

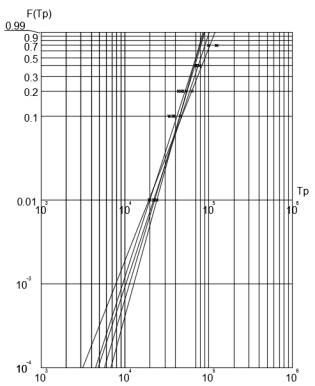
Рис.4. Распределения выборок ресурса и их генеральных совокупностей с размахом R=20

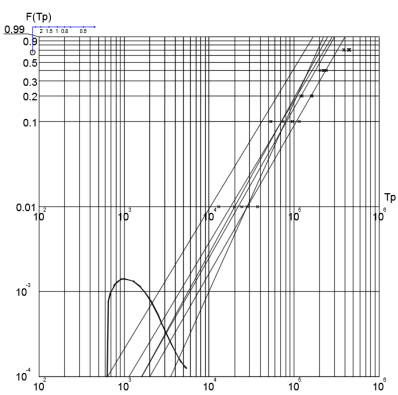
Рис.5. Распределения выборок ресурса и их генеральных совокупностей с размахом R=50

Полученные значения ресурсов представлены в таблице.

Таблица

Результаты расчета минимального ресурса деталей

Rв	Трс min	Трс max	Rс	Ку.р.
1,25*	41	49	1,2	-
20	3100	6800	2,2	6,45
50	620	3500	5,64	32,26

* - размах твердости стали

Коэффициент увеличения ресурса

,

(1)

где – фактический минимальный ресурс серийной детали, требующий увеличения .

Рис.6. Увеличение заданного ресурса Тр_зад до Тр_с1 для гарантии «ноль» отказов

Ранее проведенными исследованиями [7,8] предложен графический метод, позволяющий определять значения ресурса детали, основываясь на расчетных данных. Он позволяет осуществить переход от выборочных данных к данным генеральной совокупности конечного объема.

В представленной работе при проведении расчетов использовались выборочные распределения ресурса деталей в интервале F(x)=0,01-0,99, т.е. для единой базы сравнения вероятностных распределений с разными относительными размахами.

Результаты моделирования представлены на рис. 1 с использованием вероятностной бумаги (сетки) для закона Вейбулла со сдвигом с тремя параметрами [6].

Рис. 6. Блок-схема алгоритма графо-аналитического определения параметров совокупностей

По принципу построения видно, что параметр масштаба а выборки равен параметру масштаба А совокупности (см. рис. 1), а параметр формы b выборочного распределения равен параметру формы B генеральной совокупности конечного объема, а вместо параметра сдвига следует принимать наименьшее значение ресурса, Х_1с, так как в интервале 0 ÷ Х_1с отсутствуют отказы (имеет место абсолютная безотказность).

После нанесения точек выборочного распределения (кумуляты) построена аппроксимирующая прямая в интервале F(x)=0,01-0,99.

При помощи графического способа нахождения параметров распределения были определены выборочные параметры масштаба а, формы b и параметра сдвига с.

В результате продления прямой выборочного распределения, например, в интервале F(x)= 10^-4 -0,9₄ получили прямую распределения генеральной совокупности конечного объема N_c=10⁴.

График, представленный на вероятностной сетке, разбит на три части: верхняя часть F(x)=0,99-0,9₄ является продолжением средней части выборочной прямой при F(x)=0,01-0,99 и считается верхней частью распределения генеральной совокупности конечного объема.

Продолжение прямой выборочного распределения в нижней части графика в интервале F(x)=0,01-10^-4 является началом генеральной совокупности конечного объема. Первое значение вариационного ряда совокупности

(2)

Для проверки принадлежности полученных выборочных прямых к исходной совокупности проведен расчет параметров выборочных рядов путем компьютерного моделирования. Найденны выборки объемом n=100 в количестве m=50 штук с различными размахами: R=1,25, 20, 50. Далее для каждой выборки определены параметры соответствующей ей совокупности. Но, так как ранее говорилось о том, что численно значения параметров масштаба и формы выборки равны параметрам совокупности (а=А, b=B), а вместо параметра сдвига совокупности рассматривается первое значение вариационного ряда, то сравнению подвергались только Х_1с.

Преимуществом графического решения задачи о замене выборки совокупностью и более полного учета числа отказов является графическое совпадение на вероятностной бумаге закона Вейбулла для прямых совокупности и выборки. При этом параметры формы и масштаба для совокупности и выборки численно равны, а первые значения выборочных рядов лежат на одной прямой.

Таким образом, изложенный метод определения параметров выборочного и совокупности конечного объема распределений Вейбулла позволяет обеспечить гарантию высокой или даже абсолютной безотказности деталей.

Литература

1. Касьянов В.Е. Испытание экскаваторов в эксплуатации и расчет показателей их надежности на ЦВМ //Надежность и контроль качества. – 1976. - №6. С.15-19.

2. Уилкс С. Математическая статистика. М.: Наука, 1967, 632 с.

3. Крамер Г. Математические методы статистики .Под ред. А.Н. Колмагорова. М.: Мир, 1975, 648 с.

4. Справочник по надежности. Применение математических и статистических методов для исследования наджности и долговечности. О.Б. Моун. М.: Мир, 1969, с108-206.

5. Графические методы обработки данных. Метод вероятностных сеток [Текст]: ГОСТ 11.008-75. – Введ. 1976-07-01. – М.:Изд-во стандартов, 1975, 40с.:ил.

6. Kapur K.C., Lamberson L.R. Reliability in Engineering Design. Departament of Industrial Engineering and Operations Research Wayne State University Detroit, Michigan 48202, 1977.

7. Касьянов В.Е., Теплякова С.В. Обеспечение абсолютной безотказности деталей за заданный ресурс // Научный журнал «Научное обозрение» №9 2014, часть 3

8. Теплякова С.В. Метод графо - аналитического определения параметров закона Вейбулла // Научный журнал «Научное обозрение» №11 2014, часть 2