Techniczne nauki / 6. Electrical engineering and electronics
Candidate of Technical Sciences Sukhar'kov O.V.
Odessa National Academy of Telecommunication named
after O.S. Popov,Ukraine
Sound generation in
the modified hydrodynamic radiator
Currently stream hydrodynamic radiators
(HDR) are used to enhance the efficiency
of various physical processes [1, 2]. Among the
advantages of data converters there are high energy intensity (the ratio of radiated power
to mass), low cost of radiators manufacture, small
size and simple maintenance. Stream HDRs are
conventionally divided into uniflow and counterflow converters [1]. For HDRs of
the two types the sound generation mechanism is explained by pulsations of
localized two-phase region and transverse bending self-oscillation of
axisymmetric jet shell [3]. The author designed and developed a modified HDR with a step obstacle and circular gap nozzle in the form of coaxial discs [4].
In the modified HDR flat
submerged axisymmetric jet interacts with a stepped obstacle, which has square niche
in front of it [4]. The process of sound generation in the interaction of the incoming flow with a
rectangular niche is analyzed [5 – 8]. In the case of
small flow rates ![]() , when the Reynolds number
, when the Reynolds number ![]() (
(![]() – kinematic liquid viscosity) does not exceed
– kinematic liquid viscosity) does not exceed ![]() there are stable
vortices formed inside the niche (one or two). With
this flow mode around the niche
no effects associated with the generation of sound arise. Significant increase in
Reynolds number leads to oscillation of the vortex at the aft wall of the niche
and related vertical oscillation of the shear layer over the niche with a certain
period
there are stable
vortices formed inside the niche (one or two). With
this flow mode around the niche
no effects associated with the generation of sound arise. Significant increase in
Reynolds number leads to oscillation of the vortex at the aft wall of the niche
and related vertical oscillation of the shear layer over the niche with a certain
period ![]() . Frequency of acoustic oscillations excited by the flow is substantially
proportional to the flow velocity and inversely proportional to the length of
the niche. This confirms the fact that the niche being flown around may be referred
as an acoustic generator, in which some part of the flow self-oscillations is excited
by aerohydrodynamic feedback [5, 8].
. Frequency of acoustic oscillations excited by the flow is substantially
proportional to the flow velocity and inversely proportional to the length of
the niche. This confirms the fact that the niche being flown around may be referred
as an acoustic generator, in which some part of the flow self-oscillations is excited
by aerohydrodynamic feedback [5, 8].
At higher Reynolds numbers (about ![]() ) it was found that in
addition to the above mentioned mechanism of sound generation, there is another
mechanism associated with abrupt periodic release of vortex from niche into the
flow [5]. The reason of the phenomenon is the ongoing oscillations
of the shear layer that last for some time while the layer is swept away by
flow beyond the niche. In English literature the mechanism is known as “wake
mode”. Feedback mechanism in the
self-oscillatory system has purely hydrodynamic nature [7]. However, in the
modified HDR an other kind of oscillation mode feedback is
implemented in comparison to the case of
the interaction of incoming flow and niche. This is due to the forming of two-phase
medium in the rectangular niche of HDR (liquid and steamgas microbubbles).
) it was found that in
addition to the above mentioned mechanism of sound generation, there is another
mechanism associated with abrupt periodic release of vortex from niche into the
flow [5]. The reason of the phenomenon is the ongoing oscillations
of the shear layer that last for some time while the layer is swept away by
flow beyond the niche. In English literature the mechanism is known as “wake
mode”. Feedback mechanism in the
self-oscillatory system has purely hydrodynamic nature [7]. However, in the
modified HDR an other kind of oscillation mode feedback is
implemented in comparison to the case of
the interaction of incoming flow and niche. This is due to the forming of two-phase
medium in the rectangular niche of HDR (liquid and steamgas microbubbles).
The proposed physical
model of HDR is
based on the idea of self-oscillations of submerged circular jet
plate in the presence of developed
cavitation (fig. 1).
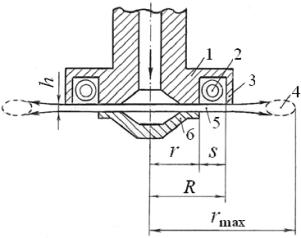

à b
Fig.1. Modified
HDR: a – physical
model
b – photo of operating
radiator
Submerged axisymmetric jet 5
(fig. 1a) outflows perpendicularly to the axis of the radiator
from the slit nozzle radiator that is formed by coaxial discs of body 1 and
fairing 6. The jet is a kind of an elastic circular jet plate that makes
bending oscillations. We can assume that the inner edge of an circular plate is
rigidly clamped at the nozzle exit and the outer edge leans freely against the
stepped obstacle 3. Among the geometric parameters of the jet plate there are:
thickness ![]() , width
, width ![]() , inner radius
, inner radius ![]() and an outer radius
and an outer radius ![]() . Moreover, the plate thickness
. Moreover, the plate thickness ![]() is small in comparison to the
radius
is small in comparison to the
radius ![]() . Hydrodynamic parameters of jet plate are:
. Hydrodynamic parameters of jet plate are: ![]() – density, equivalent module of elasticity of a submerged jet and
its velocity at the nozzle exit. A niche with almost square cross-section is
made in the body 1 of the radiator. Stepped obstacle 3 (rectangular wedge) helps
to ensure that due to the Bernoulli effect a part of the kinetic energy of the
jet is spent on the formation of primary toroidal vortex 2 in the niche. In the
center of the vortex region 2, the conditions for the cavitation are created. Therefore the niche is filled with two-phase
medium (liquid and steamgas microbubbles).
– density, equivalent module of elasticity of a submerged jet and
its velocity at the nozzle exit. A niche with almost square cross-section is
made in the body 1 of the radiator. Stepped obstacle 3 (rectangular wedge) helps
to ensure that due to the Bernoulli effect a part of the kinetic energy of the
jet is spent on the formation of primary toroidal vortex 2 in the niche. In the
center of the vortex region 2, the conditions for the cavitation are created. Therefore the niche is filled with two-phase
medium (liquid and steamgas microbubbles).
With increase of cavities
concentration the pressure inside of the niche increases and reaches critical
value. At this point, the deformation of the outer edge of the circular jet
plate and release of the contents of the cavitation region 2 to the external
environment takes place. This creates a secondary toroidal region 4 with
developed cavitation (fig. 1b). Cavitation bubbles
collapse in region 4 thus resulting in microshock waves in the surrounding
liquid medium. This leads to an increase of the generated acoustic signal.
After the cavities ejection the pressure inside the niche becomes smaller than
the hydrostatic pressure in the environment and the conditions for the vortex
formation are again formed in the niche. Further the described process repeats
periodically and pulsations of two-phase region 2 excite bending oscillations
in jet plate 5. Frequency
of
pulsations of cavitation region 2 depends on the jet velocity at the nozzle
exit. When the frequency of pulsations of region 2 and the proper frequency of
the jet plate 5 are the same the sound signal of maximum
level will be generated [4].
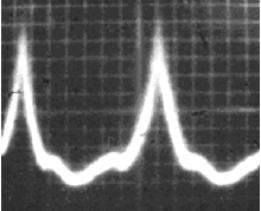
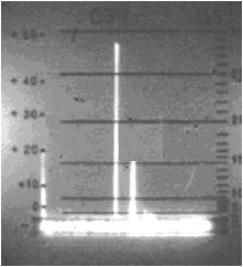
Fig. 2 demonstrates a sound
record and spectrum of typical sound signals generated
by HDR with optimal geometric
parameters and the optimum mode
of jet discharge. It is clear
(fig. 2a), that in this
case the radiator generates nonharmonic
acoustic signals in the form of short exponential
pulses. A significant fraction of the radiated sound energy falls on the fundamental frequency ![]() (fig. 2b). It has been found that the
radiator can be a source of powerful acoustic waves in the low sound frequencies
(fig. 2b). It has been found that the
radiator can be a source of powerful acoustic waves in the low sound frequencies ![]() [4].
[4].
à b
Fig.2. Typical sound
record (a) and the corresponding spectrum (b)
of the acoustic signal
from modified HDR
The
experimental investigations of HDR helped to reveal a
number of differences of sound generation in comparison with sound generation in
the interaction of the incident flow with a rectangular niche. First, in case
of the modified HDR fluid flow is formed by slit nozzle as
an elastic jet with small thickness ![]() [4]. Secondly, the radiator operates in the speed range
[4]. Secondly, the radiator operates in the speed range ![]() that results in the formation of cavitation area in the niche.
Thirdly, a modified HDR generates sound signal at a very
high Reynolds numbers:
that results in the formation of cavitation area in the niche.
Thirdly, a modified HDR generates sound signal at a very
high Reynolds numbers: ![]() . Furthermore, with increase of the jet velocity at constant geometrical
parameters of HDR the frequency of the main sound tone
generated by the HDR decreases. The latter fact is contradicts
completely to the classical laws that are specific to a aerohydrodynamic sound radiators.
. Furthermore, with increase of the jet velocity at constant geometrical
parameters of HDR the frequency of the main sound tone
generated by the HDR decreases. The latter fact is contradicts
completely to the classical laws that are specific to a aerohydrodynamic sound radiators.
To answer the
question, what makes a flat axisymmetric jet perform strictly periodic
oscillations, i.e. operate in a self-oscillation mode, we use the analysis of article [3]. Since the wave size of oscillating circular jet
plate is substantially smaller than the wavelength, its outer surface is loaded
by an impedance that has mainly mass character. In contrast, the inner surface
of the plate is loaded by an impedance having an elastic nature. Moreover, due
to the rather high ductility of two-phase medium, the corresponding elasticity
may be relatively small. As the result a kind of resonance acoustic system
consisting of three series-connected elements: elasticity – jet plate – mass is created. Clear enough, it
has its proper frequency, which will be imposed on the transverse oscillations
of an circular plate. This is the physical mechanism of self-oscillation
feedback of jet plate, the nature of which in this case is purely acoustic.
Literature:
1. Dudzinski Yu. M.
Axial-symmetric hydrodynamic radiators used for fluid cavitation threshold
measurement / Yu. M. Dudzinski, O. V. Sukharkov, N. V. Manicheva // The IVth
International Hutsulian Workshop on Mathematical Theories and their
Applications in Physics & Technology, 28 October–02 November 2002: The
materials of conf. – Kyiv: TIMPANI, 2004. – P. 275 – 286.
2. Ñóõàðüêîâ Î.Â. Ïåðåäà÷à äèñêðåòíîé èíôîðìàöèè â ãèäðîàêóñòè÷åñêèé êàíàë
ñâÿçè ñ èñïîëüçîâàíèåì æèäêîñòðóéíûõ ïðåîáðàçîâàòåëåé / Î.Â. Ñóõàðüêîâ // Öèôðîâ³
òåõíîëî㳿. – 2011. – ¹ 9. – Ñ. 100 – 110.
3. Âîâê È.Â. Î âîçìîæíîì ìåõàíèçìå àâòîêîëåáàíèé
â ñòðóéíûõ ãèäðîäèíàìè÷åñêèõ èçëó÷àòåëÿõ ñ ðàçâèòîé êàâèòàöèåé / È.Â. Âîâê, Â.Ò.
Ãðèí÷åíêî, Þ.Ì. Äóäçèíñêèé // Àêóñòè÷íèé â³ñíèê. – 2008. – 11, ¹ 2. – Ñ. 16 – 23.
4. Ñóõàðüêîâ Î.Â. Àêóñòè÷åñêèå
ñâîéñòâà ìîäèôèöèðîâàííîãî
æèäêîñòðóéíîãî ïðåîáðàçîâàòåëÿ â óñëîâèÿõ ãèäðîñòàòè÷åñêîãî äàâëåíèÿ / Î.Â. Ñóõàðüêîâ //
Ýëåêòðîíèêà è ñâÿçü. – 2012. – ¹ 5(70). – Ñ. 77
–
87.
5. Krishnamurty K. Sound radiation from
surface cutouts in high speed flow. PhD thesis / K. Krishnamurty. – California : Inst.
Technol. Press, 1956. – 76 p.
6. Higdon J.J.L. Stokes flow in arbitrary two-dimensional: shear flow
over ridges and cavities / J.J.L.
Higdon // J. Fluid Mech. – 1985. – N 159. – P. 195 – 226.
7. Rowley C.W. On self-sustained oscillations in two-dimensional compressible flow
over rectangular cavities / C.W. Rowley, T. Colonius, A.J. Basu // J. Fluid Mech. – 2002. – N 455. – P. 315 – 346.
8. Larcheveque D.L. Large-Eddy Simulation of flows past cavities / D.L. Larcheveque, P. Comte, P. Sagaut // Southampton, February 25. – AFM research group seminar, 2004. – P. 13 – 21.