построение 3D графиков при нижнем давлении

Пиль Э.А.

Академик РАЕ, профессор, доктор технических наук,

г. Санкт-Петербург

В представленной ниже статье рассмотрен вопрос влияния трех переменных на ВВП (GDP) и представление их в трехмерном пространстве. Они позволяют более полно представить влияние различных переменных на ВВП (GDP). При этом переменные являются постоянными и увеличиваются. То есть, в предлагаемой статье рассмотрена зависимость изменения ВВП (GDPsl) = f(Х1, Х2, Х3).

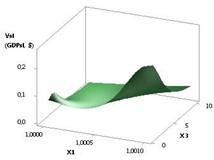
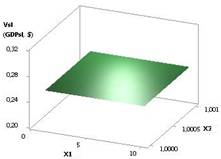
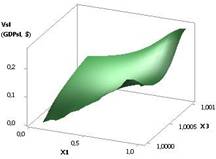
На первом рис. 1 показана зависимость GDPsl при Х1 = Х2 = 1 и Х3 = 1…10. Из данного рисунка видно, что значения ВВП (GDPsl) уменьшаются со значения 0,26 до своей минимальной величины GDPsl = 0,008, т.е. в 31,62 раза.

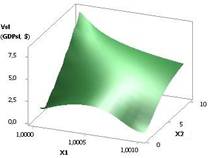
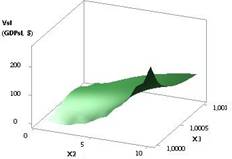
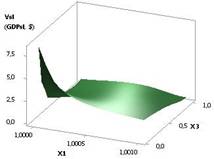
Рис. 1. ВВП (GDPsl) = f(X1, Х3) при Х1 = Х2 = 1, Х3 = 1…10	Рис. 2. ВВП (GDPsl) = f(X1, Х2) при Х1 = 1, Х2 = Х3 = 1…10
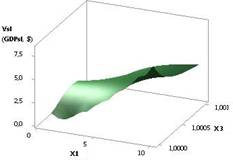
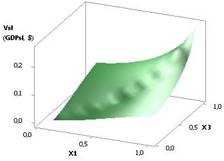
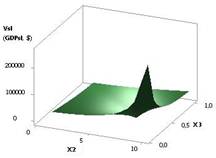
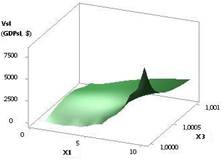
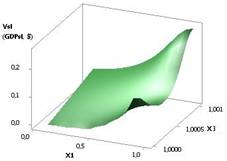
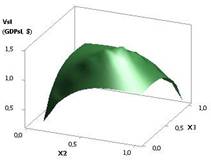
Рис. 3. ВВП (GDPsl) = f(X1, Х3) при Х1 = 1…10, Х2 = Х3 = 1	Рис. 4. ВВП (GDPsl) = f(X1, Х3) при Х1 = Х2 = 1…10, Х3 = 1

Следующий рис. 2 дает наглядное представление, что при значениях переменных Х1 = 1 и Х2 = Х3 = 1…10 построенная 3D зависимость увеличивается в 31,62 раза, начиная с 0,26 и до 8,16.

На следующих двух рисунках 3 и 4 показаны зависимости GDPsl = f(Х1, Х3), когда переменные были Х1 = 1…10, Х2 = Х3 = 1 и Х1 = Х2 = 1…10, Х3 = 1 соответственно. Значения GDPsl на рис. 4 достигают достаточно большой величины 8160,84.

Рис. 5. ВВП (GDPsl) = f(X1, Х2) при Х1 = Х3 = 1…10, Х2 = 1		Рис. 6. ВВП (GDPsl) = f(Х2, Х3) при Х1 = Х3 = 1, Х2 = 1…10
Рис. 7. ВВП (GDPsl) = f(X1, Х3) при Х1 = Х2 = Х3 = 1…0,1	Рис. 8. ВВП (GDPsl) = f(X1, Х3) при Х1 = Х2 = 1…0,1, Х3 = 1

Следующие два рисунка 5 и 6 были построены при Х1 = Х3 = 1…10, Х2 = 1 и Х1 = Х3 = 1, Х2 = 1…10. Из рисунков видно, что изображенные кривые GDPsl либо имеют постоянные значения (рис. 5), либо увеличиваются до 258,07 с 0,26, т.е. в 1000 раз (рис. 6).

Для построения двух 3D графиков на рис. 7 и 8 были использованы следующие значениях переменных Х1 = Х2 = Х3 = 1…0,1 и Х1 = Х2 = 1…0,1, Х3 = 1. В этих примерах кривые GDPsl имеют одинаковый вид, уменьшаясь с 0,26 до 0,0003 и 8,16E-06 соответственно.

Построенная зависимость GDPsl на рис. 9 при Х1 = 1…0,1, Х2 = Х3 = 1 уменьшается практически по линейной зависимости с 0,26 до 0,01.

Из следующего рис. 10 видно, что кривая GDPsl при переменных Х1 = Х2 = 1, Х3 = 1…0,1 увеличивается с 0,26 до 8,16.

Рис. 9. ВВП (GDPsl) = f(X1, Х3) при Х1 = 1…0,1, Х2 = Х3 = 1		Рис. 10. ВВП (GDPsl) = f(X1, Х3) при Х1 = Х2 = 1, Х3 = 1…0,1
Рис. 11. ВВП (GDPsl) = f(Х2, Х3) при Х1 = Х2 = 1…10, Х3 = 1…0,1	Рис. 12. ВВП (GDPsl) = f(Х2, Х3) при Х1 = 1…10, Х2 = Х3 = 1…0,1

На последних двух рисунках 11 и 12 были построены две трехмерные области GDPsl при Х1 = Х2 = 1…10, Х3 = 1…0,1 и Х1 = 1…10, Х2 = Х3 = 1…0,1 соответственно.

Здесь на рис. 11 построенная кривая GDPsl достигает очень значительной величины 258068,36, увеличившись в 1000000 раз по отношению к своему начальному значению.

Симметричная кривая GDPsl, представленная на рис. 12 имеет максимумы 1,34 в точках 5 и 6.