Математика/4. Прикладная математика
К.ф.-м.н. Зинченко А.Б., Иванина А.А.
Южный федеральный университет. Россия
Кооперативные
игры, моделирующие инвестирование
Объединяя капиталы, инвесторы получают
возможность вкладывать средства в проекты, увеличивающие выплаты, но
недоступные им без сотрудничества. Возникают взаимосвязанные проблемы:
формирование наиболее перспективных коалиций; оптимальное распределение
капитала между возможными инвестиционными проектами; выбор способа дележа
совместно заработанной прибыли, устраивающего каждого из партнеров. В
литературе описаны различные классы игр, моделирующих коллективное инвестирование:
однопериодные депозиты [1]; многопериодные депозиты без реинвестирования [2] и с
реинвестированием [3]; инвестиционные проекты с дискретными вкладами [3]. Нечеткие
инвестиционные игры рассматривались в [4]-[6]. При исследовании нечетких игр,
основное внимание уделялось обобщению концепции С-ядра и выводу условий его
существования.
В данной статье описаны два специальных класса инвестиционных игр: игры с ограниченной кооперацией и полусимметричные игры с
дискретными вкладами. Для первого класса игр предложены способы вычисления характеристических
функций (четкой и нечеткой). Показано, что существуют инвестиционные игры, в
которых вес оптимальной нечеткой структуры больше, чем вес любой четкой
структуры и больше веса максимальной коалиции. Для второго класса игр выведена
формула, явно определяющая характеристическую функцию.
В классической кооперативной игре
, где 
, 
, 
, (четкой) коалицией является любое подмножество 
множества игроков. Четкой
коалиционной структурой
, 
, 
,
называется разбиение 
на непустые попарно
непересекающиеся коалиции. Если игроки участвуют в нескольких коалициях одновременно,
то используется понятие нечеткой коалиции 
, где 
- степень участия
игрока i в коалиции 
. Нечеткая кооперативная игра [7] 
определяется функцией 
, 
. Нечеткая коалиционная структура имеет вид
, 
, 
.
Модель 1 (без ограничений). Пусть: - множество инвесторов;
; 
- вектор капиталов; 
- множество
инвестиционных проектов; 
- вектор минимальных допустимых
вкладов в проекты; 
- количество денег,
вкладываемых коалицией 
в проект 
; 
- функция доходности 
-го проекта. Инвестиционный план 
коалиции 
допустим, если сумма
инвестиций во все проекты не больше суммарного капитала участников коалиции. Максимальное количество денег 
, которое может получить коалиция в результате инвестирования,
определяется капиталом 
этой коалиции
. (1)
Если некоторые из игроков, образовавших коалицию,
используют для инвестирования только часть своих капиталов, т.е. 
, то 
определяется капиталом
нечеткой коалиции
. (2)
Заметим, что в играх и , определенных задачами (1)-(2), допустимы: зависящие от
времени депозиты; зависящие от капитала депозиты; срочные вклады, выплата
процентов по которым производится после фиксированного количества периодов времени.
Предполагается, что вклады в многопериодные проекты осуществляются в начале
первого периода. Если нужно учитывать реинвестирование и/или инвестирование в
ценные бумаги, то задачи (1) и (2) модифицируются. В частности, в них
появляются дискретные переменные.
Пример 1. Рассмотрим ситуацию двухгодичного инвестирования с тремя участниками
(капиталы 800, 300 и 400 д.е.) и тремя проектами:
-
двухлетний срочный вклад (сумма вклада не меньше 1000 д.е., ставка по
вкладу 2%);
-
срочный вклад на первый период (сумма вклада не меньше 500 д.е., ставка по
вкладу 0.8% годовых),
-
реинвестирование всех денег, полученных на первом этапе (ставка 0.8% ).
В данном случае: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
. В инвестиционных планах 
коалиций 
переменная 
- дискретная 
. Она имеет отличную от 
интерпретацию: 
при реинвестировании и
в противном случае. Используя
, 
, 
и задачу
,
, , ,
получаем четкую игру трех лиц, значения характеристической
функции которой приведены в таблице 1. Предположим теперь, что первый и второй
игрок собираются использовать для инвестирования 
часть своих капиталов,
а третий игрок – весь капитал. Тогда
, 
, 
(оптимальный
инвестиционный план 
). ►
Модель 2 (игра с ограниченной кооперацией).
При формировании объединений в многоагентных системах не все коалиции бывают
возможными. Ограничения на образование коалиций возникают при отсутствии коммуникаций,
нежеланием некоторых игроков сотрудничать друг с другом или правом вето,
позволяющим какому-либо из игроков запретить коалиции без его участия. В связи
с этим, в игру вводят математический
объект 
, содержащим дополнительную информацию. может быть
коалиционной структурой, гиперграфом, матроидом. Наиболее изученными являются
игры 
[8], где 
- неориентированный
граф с множеством вершин и множеством ребер 
. Допустимыми являются коалиции , соответствующие связным подграфам 
графа 
. Функция 
определена на
множестве допустимых коалиций. Для вычисления решения игры используется вспомогательная
игра без ограничений 
, где 
равно сумме значений
функции для компонент связности
подграфа 
.
Таблица 1
Инвестиционная ситуация из примера 1
|
Коалиция |
Капитал |
|
Оптимальный инвестиционный план |
|
|
800 |
812.8512 |
|
|
|
300 |
0 |
|
|
|
400 |
0 |
|
|
|
1100 |
1122 |
|
|
|
1200 |
1224 |
|
|
|
700 |
711.2448 |
|
|
|
1500 |
1530 |
|
Рассмотрим инвестиционную игру 
, где 
- список запрещенных
коалиций 
. Для не подходит описанный выше способ вычисления характеристической
функции вспомогательной игры . В игре без запретов 
, соответствующей , положим 
для запрещенной
коалиции 
равным весу оптимальной
структуры, являющейся разбиением на допустимые подкоалиции.
Пример
2. Пусть 
,
и 
. Возьмем 
. Коалиции соответствует связный граф
, где
. Поэтому 
. Но в данной игре значение 
не определено, т.к. 
. Три из возможных разбиений множества на непересекающиеся
подмножества не содержат запрещенных коалиций: {{1},{2},{3}}, {{12},{3}},
{{23},{1}}. Значит,
. ►
Инвестиционная игра 
состоит из
нечеткой игры и списка запрещенных носителей нечетких коалиций 
, где 
. В вес коалиции с запрещенным носителем 
положим равным весу оптимальной нечеткой
структуры с допустимыми носителями, содержащимися в .
Пример 3. Рассмотрим ситуацию, отличающуюся от ситуации, описанной в примере 1
капиталами инвесторов (700, 700 и 600 д.е.) и запретом на формирование коалиций
и , т.к. между первым и вторым игроками существуют отношения,
исключающие их сотрудничество. В соответствующей игре : , 
. Значения функции 
вспомогательной игры приведены в
таблице 2. Проверим, могут ли игроки увеличить доход от инвестирования,
образовав коалиционную структуру. Все возможные
четкие структуры 
игры трех лиц
приведены в таблице 3. Вес оптимальной структуры равен 2037.2448. Рассмотрим
нечеткую коалиционную структуру 
, не содержащую компоненты с запрещенными
носителями. Суммарный капитал равен 
. Вес нечеткой структуры 
больше,
чем вес любой четкой структуры. ►
Таблица 2
Инвестиционная ситуация из примера 3
|
Коалиция |
Капитал |
|
Оптимальный инвестиционный план |
|
|
700 |
711.2448 |
|
|
|
700 |
711.2448 |
|
|
|
600 |
609.6384 |
|
|
|
1400 |
1422.4896 |
|
|
|
1300 |
1326 |
|
|
|
1300 |
1326 |
|
|
|
2000 |
2037.2448 |
|
Таблица 3
Четкие структуры для игры из примера 3
|
Структура |
{{1},{2},{3}} |
{{12},{3}} |
{{13},{2}} |
{{23},{1}} |
{{123}} |
|
Вес |
2032.128 |
2032.128 |
2037.2448 |
2037.2448 |
2037.2448 |
Модель 3 (полусимметричная игра с дискретными
вкладами). Рассмотрим ситуацию с двумя инвестиционными проектами (10% банковский
депозит; 20% вклад, который должен быть кратным 100 д.е.) и 
инвесторами, располагающими
капиталами 10
, …, 10
, где , …, - целочисленные
параметры, удовлетворяющие условиям: 
=
= …=, 
, 
, 
. Эта ситуация обобщает пример 5 из [3] (стр. 92). Обозначим:
- мощность коалиции , 
- целая часть числа 
. Для каждой коалиции :
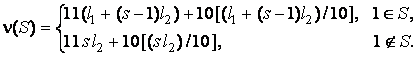
После 0-нормализации игры 
получаем:
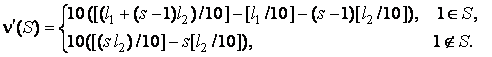
Игра монотонна, но ее
С-ядро 
может быть пустым. Если 
, то игра имеет также непустое симметричное ядро [9]. Одним
из достаточных условий сбалансированности монотонной игры является наличие ней
или в ее 0-форме вето игрока. Из приведенных выше формул следует, что игра 
с девятью и более участниками
не имеет вето игроков. Если 
и параметр 
принадлежит одному из
полуоткрытых интервалов
, 
, 
,
то в есть вето игрок. В
частности, для игры трех лиц, первый инвестор имеет право вето тогда и только
тогда, когда: 
или 
или 
или 
и т.д.
Литература:
1. Izquierdo J., Rafelse C. A generalization of the bankruptcy
games: financical cooperative games // Working paper
E96/09.
2. Bonn P., Waegenaere A., Rafels C., Suijs J.,
Tijs S., Timmer J. Cooperation in capital deposits // OR Spektrum.
2001. V.23. P.265-281.
3. Waegenaere A.M.B., Suijs J.P.M., Tijs S.H. Stable profit
sharing in cooperative investments // OR Spectrum. 2005. V.27. No.1. P.85-93.
4. Azrieli Y., Lehrer E. Cooperative investment games
or population games // Game Theory and
Information 0503007. Economics Working Paper Archive at WUSTL. 2005.
5. Fukuda E., Ishihara S., Muto S., Tijs S., Branzei R. Cooperative fuzzy games arising
from economic situations // Fuzzy Economic Review. 2005. No.1. P.3-15.
6. Molina E., Tejada J. Linear production games with
committee control: Limiting behavior of the core // European Journal of
Operational Research. 2004. V.154. P.609-625.
7. Aubin J.P. Cooperative fuzzy games // Mathematics
of Operations Research. 1981. No.6.
P.1–13.
8. Myerson R. Graphs and cooperation in
games // Mathematics of Operations Research. 1977. V.2.
P.225–229.
9. Zinchenko A.B. Symmetric core of cooperative side
payments game // Contributions
to Game Theory and Management. 2014. V.
7. P.428–437.