К. ф.-м. н. Сериков В.И., к. ф.-м. н. Воронин С.В.

Липецкий государственный технический университет, Россия

О связи решений обобщённого уравнения Бюргерса с решениями уравнения Кортевега – де Вриза и кубического уравнения Шрёдингера.

Уравнения Бюргерса и уравнения Кортевега – де Вриза (КдВ) в нелинейной акустике имеют вид [1]

(1)

где α - постоянная поглощения, а ε - нелинейная постоянная,

(2)

где β - параметр дисперсии, а величина v и константа c имеют смысл скорости. Переходя в этих уравнениях к безразмерной скорости , запишем уравнения (1) и (2) в виде

(3)

(4)

Пространственная переменная x и переменная , где - временная переменная, имеют одинаковую размерность, что позволяет рассмотреть ещё одну замену , и записать уравнения в форме

(5)

(6)

В уравнении (6) сделаем замену , тогда имеем

(7)

Выполним теперь преобразование , , , тогда уравнение (7) можно записать в форме

(8)

Уравнение (8) представляет собой уравнение КдВ для функции и его можно рассмотреть совместно с модифицированным уравнением (мКдВ)

(9)

Как показал Миура  [2] соотношение

(10)

позволяет представить связь уравнений КдВ и мКдВ в виде

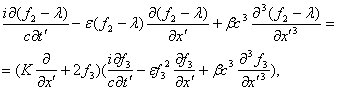, (11)

где . В соотношении (10) , применяя подстановку Хопфа – Коула

, (12)

имеем

. (13)

Соотношение (13) представляет собой уравнение типа стационарного уравнения Шрёдингера (УШ), Стационарному УШ отвечает обобщённое уравнение Бюргерса с потенциальной энергией. Легко установить, что потенциальной энергии в УШ отвечает величина , а значениям полной энергии . Соответствующее уравнение Бюргерса имеет вид [3]

, (14)

где . Поскольку аргумент t играет в функции роль параметра [4] , то величина U рассматривается, как не зависящая от времени τ, фигурирующего в стационарном УШ, решения которого имеют вид , а подстановка Хопфа – Коула в этом случае приводит к функциям вида . С учётом энергетических соотношений, уравнение (14) можно записать в форме

. (15)

Рассмотрим решение КдВ в виде уединённой волны [2]

, (17)

где , .

Уравнение (15) имеет первый интеграл, который можно записать в виде

. (16)

Это уравнение позволяет найти решения обобщённого уравнения Бюргерса, отвечающие решениям уравнения Кортевега – де Вриза.

Тогда решения (16) можно искать в виде .

Подстановка в уравнение (16) даёт

, (18)

Что приводит к уравнениям для коэффициентов

, . (19)

Из (19) получаем , так что решение уравнения (16) имеет вид

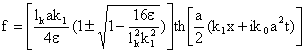, (20)

Отметим здесь, что уравнение (16) аналогично уравнению (10). Уравнения (10) привело, как известно к развитию методов обратной задачи рассеяния [5], следовательно, поиск решений обобщённого уравнения Бюргерса так же имеет отношение к этому методу.

Возвращаясь к уравнению (10) с учётом замены переменных, имеем

, (21)

, (22)

Функцию ищем в виде , где , тогда имеем 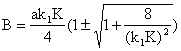, , так что амплитудный множитель определяется из энергетических соображений.

Для волновых решений с аргументом , представляет интерес ещё один аспект. Пусть, тогда , а так же

. Уравнение представляет собой уравнение Клейна – Гордона (КГ) с потенциальной энергией U [6]. Используя потенциальную энергию, определённую выше, запишем уравнение КГ в виде

, (23)

C учётом выражений для производных, имеем

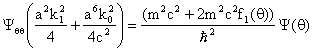, (24)

Уравнение (24) можно представить в форме

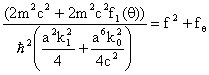, где , (25)

которое представляет собой обобщение соотношения Миура и, кроме того, показывает, что решение уравнения КдВ можно использовать, как потенциальную энергию в уравнении КГ. Отметим, что временная переменная сохраняет свой смысл, в отличии от случая рассматриваемого в работе [4].

Рассмотрим далее кубическое уравнение Шрёдингера

(26)

где . Используя подстановку , и преобразование Хопфа-Коула в уравнении (26) получаем обобщённое нелинейное уравнение Бюргерса- Шрёдингера отвечающее кубическому уравнению (26)

. (27)

Здесь - обратное преобразование Хопфа-Коула. Одним из решений кубического уравнения (26) является уединённый волновой пакет [4], который имеет вид

, (28)

где , , A- нормировочный коэффициент. В этом случае соответствующее решение обобщённого уравнения Бюргерса- Шрёдингера принимает вид

, (29)

Функция в решении (28) аналогична функции (17) , но зависимость скорости волны от амплитуды в них различна. Такое же замечание можно сделать и для решений обобщённых уравнений Бюргерса, отвечающих уравнениям (27) и (15).

Литература:

1. Красильников В.А., Введение в физическую акустику. [Текст]: Учебное пособие для физических специальностей вузов/ В.А.Красильников, В.В.Крылов. – М.: Наука, 1984. – 400с.

2. Миура Роберт М. Уравнение Кортевега – Вриза – модельное уравнение для нелинейных волн в средах с дисперсией. [Текст]:/ в сб. Нелинейные волны, под ред. С. Лейбовича и А. Сибасса, пер с англ. М. «Мир» 1977. – 319 с.

3. Сериков В.И. Квантовый подход к построению трёхмерного уравнения Бюргерса [Текст]:/ Сериков В. И., Воронин С. В. Prospekts of world science,-2015: Materials of the XI International scientific and practical conference. Volume 9. Physics. Modern information technologies. Sheffield, Science and education LTD, 2015.

4. Уизем Дж. Линейные и нелинейные волны.[Текст]: Дж. Уизем. Линейные и нелинейные волны - пер.с англ. М. «Мир», 1977. – 638 с.

5. Абловиц М. Солитоны и метод обратной задачи [Текст]:/ М. Абловиц, Х. Сигур. Солитоны и метод обратной задачи. Пер. с англ., М.: Мир, 1987. – 479 с., ил.

6. Галицкий В.М. Задачи по квантовой механике.[Текст]:Учебное пособие для физических специальностей вузов/ В.М.Галицкий, Б.М. Карнаков, В.И. Коган. - М.: Наука, 1981 г. – 648 с.