Математика/1. Дифференциальные

и интегральные уравнения

Шевчук Н.М.

Чернівецький національний університет імені Юрія Федьковича

Наближені розв’язки еволюційного рівняння гіперболічного типу

 

Багато задач математичної фізики можна подати у вигляді задачі Коші для еволюційного рівняння гіперболічного типу

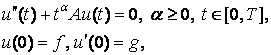                                                                        (1)

де  - невід’ємний самоспряжений оператор зі щільною областю визначення в се­­­­п­а­­­­­рабельному гільбертовому  просторі. У праці А.В.Бабина [1] методом теорії ва­­­го­вого наближення функцій на півосі одержано зображення розв’язку задачі Коші (1) у випадку  у вигляді  де  - по­лі­ном степеня  (при фіксованому ). У припущенні, що вектор  належить до о­б­л­а­с­ті визначення оператора , за шукані поліноми у вказаній роботі бе­ру­ться поліноми, які наближають функцію  на півосі з вагою . При цьому дається оцінка швидкості збіжності: похибка  спа­дає як

У книзі [2] пропонується інший метод побудови поліномів  який ба­зу­є­ть­ся на­ наближенні функцій на півосі частинними сумами їхніх рядів Фур’є, по­бу­дованими за ортогональними многочленами Лагерра, що утворюють ор­то­­-

­­­­но­­р­­­­мо­­ваний базис у просторі  де , а  - число, за­­­­лежне від вектора . Цей метод дає точнішу, ніж у праці [1], оцінку від­хилення, але у вужчому класі початкових даних.

У даній роботі будуються наближені розв’язки задачі Коші для рівняння  

 

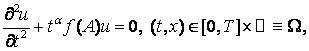
де  - деяка функція гармонійного осцилятора – оператора 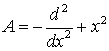. При цьому відповідні наближення є рівномірними по .

І.М.Гельфанд і Г.Є.Шилов ввели в [3] серію просторів, названих ними про­с­торами типу . Вони складаються з нескінченно диференційованих функцій, ви­­­з­­начених на , на які накладаються певні умови спадання на нескінченності і­­ зростання похідних із збільшенням порядку. Ці умови зада­ються за допо­могою нерівностей , де  - деяка подвійна по­с­­лідовність додатних чисел. Якщо на елементи послідовності   не на­кладаються жодні обмеження (тобто  можуть змінюватись довільним чином разом з функцією ), то маємо, очевидно, простір Л.Шварца швидко спадних функцій. Якщо ж числа  задовольняють певні умови, то відповідні конкретні пр­о­с­­тори містяться в  і називаються про­с­­торами типу .  Означимо деякі з них.

Для довільних  покладемо                      

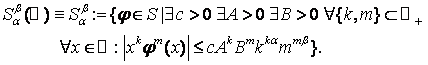
Введені простори можна охарактеризувати ще й так [3].

Простори  нетривіальні при  і утворюють щільні в  мно­жини.   Якщо  і  то  складається з тих і лише з тих функцій ,­ які допускають аналітичне продовження у всю комплексну площину і для яких               

Якщо 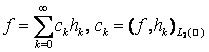 - коефіцієнти Фур’є-Ерміта, то правильними ­є­­­ наступні співвідношення еквівалентності:

а)

б)

Відомо [4], що якщо  то  де  - гармонійний осцилятор, діє на ­ за правилом    

­

Символом  позначатимемо сукупність функцій , продовжених у всю комплексну площину ; через  позначимо сукупність тих функцій  коефіцієнти Фур’є-Ерміта яких задовольняють умову б) з пара­метром .

У праці [5] доведено, що якщо ціла функція  задовольняє умову

то у просторі  визначений і є неперервним оператор , який не­пе­рервно відображає  в .

Наприклад, в  визначений і є неперервним оператор 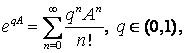   де  - гармонійний осцилятор. Якщо посилити умову на­ цілу функцію , а саме, вважати, що

то оператор  буде вже визначений на просторі  і відображатиме не­пе­­рервно цей простір в себе.

Звуження оператора  на простір  позначатимемо символом  

  Розглянемо рівняння  

                     (2)

  де  - фіксований параметр,  - оператор, побудований за функцією .

Під розв’язком рівняння (2) розумітимемо функцію , яка задовольняє умо­ви: 1)  при кожному ;  2)  двічі диференційовна по  при ко­­ж­­ному ;  3)  задовольняє рівняння (2). Відомо [6], що фундаментальну систему розв’язків рівняння  ( - число) утворюють функції      

  

де  - гама-функція,  - функція Бесселя першого роду

порядку . Зазначимо, що

.

Звідси випливає, що функція

,

де

,  , 

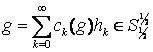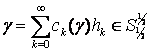є розв’язком рівняння (2), тобто розв’язком, який задовольняє початкові умови

                                       (3)

  Функції , за допомогою яких зображається розв’язок за­да­чі Коші (2), (3), мають складну структуру. Виявляється, що ці функції допускають розвинення в ряди Фур’є за ортонормованими многочленами Чебишова-Лагерра, тобто в кожній точці  правильними є  спів­відношення:        

де

 

 

 

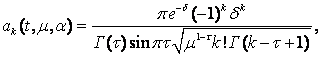
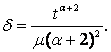
Аналогічно знаходимо, що

де

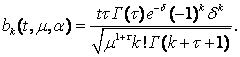
Позначимо через і частинні суми рядів Фур’є функцій  за многочленами  відповідно; при цьому   у кожній точці

Символом  позначимо сукупність тих функцій  з простору , які задовольняють умову

Правильними є наступні твердження.

Теорема 1. Нехай   - розв’язок задачі Коші (2), (3). Якщо

       то 

     де

Теорема 2. Нехай   - розв’язок задачі Коші (2), (3). Якщо  

      то 

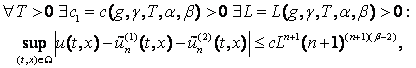
     де                                   

 

Теорема 3. Нехай   - розв’язок задачі Коші (2), (3). Якщо

       то

 

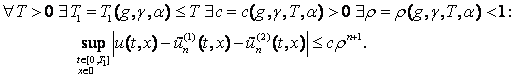
1.     Бабин А.В. Построение и исследование решений дифференциальных уравнений методами теории приближения функций // Матем. сб. – 1984. – Т.123, №2. – С.147-174.

2.     Городецький В.В. Множини початкових значень гладких розв’язків диференціально-операторних рівнянь параболічного типу. – Чернівці: Рута, 1998. – 219с.

3.     Гельфанд И.М., Шилов Г.Е. Пространства основних и обобщенных функций.  М.: Физматгиз, 1958. – 307с.

4.     Горбачук В.И., Горбачук М.Л. Граничные задачи для дифференциально-операторных уравнений. – Киев: Наук. думка, 1984. – 284с.

5.     Гома Н.М., Городецький В.В. Еволюційні рівняння з гармонійним осцилятором у просторах типу  та // Наук. вісник Чернівецького університету: Зб. наук. праць. Вип. 269. Математика. – Чернівці: Рута, 2005. – С. 13 – 25.

6.     Вайнерман Л.И. Гиперболические уравнения с вырождением в гильбертовом пространстве // Сиб. мат. журн. – 1977. Т. 18, №4. – С. 736 – 746.