Математика

Прикладна математика

Василенко Ю.А., Копча Г.Е.

(Закарпатський державний університет)

АЛГЕБРАЇЧНИЙ ОПИС ДЕЯКИХ К-МНОГОВИДІВ

Існує аналогія між класами алгебр і алгоритмічними схемами (стосовно операцій), з якої випливає такий висновок: будь-яка сукупність алгоритмічних схем повинна визначати певний клас алгебр. Тому досить цікавою проблемою є проблема вивчення класів алгебр, в основі яких лежать типові алгоритмічні схеми.

Розглянемо деякі алгебри та класи алгебр. К-многовид – це клас алгебр, який визначається певною сукупністю схем. Матимемо на увазі клас всіх алгебр виду [М,К], де К – деяка множина схем, відносно якої система М замкнута, множина К фіксована, і будемо називати його К-многовидом.

В статті [1] одержано алгебраїчне описання К-многовидів виду [М,К₁] і [М,К₂], де МZ^¢(G) (Z^¢(G)=Ф^¢(G)ÈR^¢(G), Ф^¢(G) – множина всіх всюди визначених операцій на деякій множині G, R^¢(G) – множина всіх всюди визначених предикатів на цій множині, К – деяка множина схем, f_i Î Ф^¢(G), p_jÎR^¢(G)), К₁={p(f₁,f₂)} і К₂={f₁f₂, p(f₁,f₂)}.

Алгебри із многовидів [М,К₁] і [М,К₂], відповідно, називатимемо алгебрами і предикатними напівгрупами.

При вивченні предикатних алгебр будемо розглядати замість відображень f_і: G®G більш загальні відображення f_і: G®В, де G і В – довільні множини.

Нехай – множина всіх відображень множини G в В. Будь-який одномісний предикат р(х) над G задає деякий двохмісний оператор на множині , який визначається таким чином:

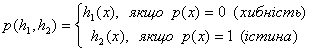(1)

Тут . Очевидно, що . Оператор (1) називається предикатним оператором. Будемо вважати, що при записуванні предикатного оператора у виді символ р означає відповідний предикат.

Система відображень замкнута відносно предиката р, якщо з випливає . Система Н замкнута відносно системи предикатів із , якщо Н замкнута відносно всіх предикатів із . Сукупність предикатів і замкнутої відносно системи Н утворює деяку алгебру. Цю алгебру назвемо предикатною алгеброю. Опишемо предикатну алгебру.

Розглянемо абстрактну алгебру, яка представляє собою сукупність множин Н і заданої на Н системи L бінарних операцій (,). Операції із L задовольняють наступним тотожностям:

а) =h,

б) , (2)

в) ,

де , .

Таким чином визначену алгебру назвемо N-алгеброю. Очевидно, що всяка предикатна алгебра являється N-алгеброю.

В [1] доведена така важлива теорема.

Теорема 1. Кожна вільна N-алгебра ізоморфна деякій предикатній алгебрі.

Розглянемо вільну N-алгебру А, породжену деякою системою твірних Н і системою операцій L. Вирази вільної N-алгебри А, елементи із Н і L, відповідно, будемо називати формулами, Н-символами і L-символами. Формули і , які зображають один і той же об’єкт вільної N-алгебри А, називаються еквівалентними. Еквівалентність і нееквівалентність позначаються, відповідно, через і . Формула належить системі формул М (), якщо еквівалентна одній із формул М. Через = позначимо співпадання формул і . У вільній N-алгебрі А для кожного цілого числа визначимо формули такого виду

, де , , причому при іj.

Формули визначаються індукцією по п. Для п=0 покладаємо (0 – символ пустого кортежу ). Якщо для п формули F визначені, то для п+1 покладаємо

=(,).

Таким чином, маємо

(, =((,() і т. д.

Наслідок з теореми 1. Сукупність рівностей (2) представляє собою алгебраїчний опис класу всіх предикатних алгебр.

1. И.В.Витенько. Схемы, алгоритмы и многообразия. – Ужгород, 1970.

2. І.В.Вітенько. Конструктивні операції. – Ужгород. Уж. ун-т, 1970.

3. Ю.А.Василенко, Ф.Г.Ващук. Об алгоритмическом понятии вычислительной схемы. – Ужгород: Науковий вісник УжДІІЕП, №1, 1997.

4. Ю.А. Василенко, Г.Е.Копча. Алгоритмічна схема як алгебраїчний об’єкт // Матеріали IV Міжнародної науково-практичної конференції „Динаміка наукових досліджень ‘ 2005”. Том 50. Сучасні інформаційні технології. –Дніпропетровськ: Наука і освіта, 2005. – С. 3-5.

5. Ю.А. Василенко, Г.Е.Копча. Деякі види схем з точки зору алгебри // Матеріали IX Міжнародної науково-практичної конференції „Наука та освіта-¢2006”. Том 13. Фізика, математика. – Дніпропетровськ: Наука і освіта, 2006. – С. 57-59.