Рубашка В.П.

Украинская инженерно-педагогическая академия, г. Харьков

математическАЯ моделЬ мостовой конструкции с подвижным инерционным включением.

Целью данных исследований является развитие методов анализа колебаний упругой мостовой конструкции, несущей подвижное инерционное включение. Считается, что подвижная инерционная нагрузка в каждый момент времени разбивает пролет несущего строения на элементы переменной длины. Для получения решений вводятся нестационарные дискретные модели, которыми представляются, элементы переменной длины. В качестве метода дискретизации выбран метод конечных элементов, преимущества которого в определении параметров дискретной схемы наиболее ярко проявляются для систем с зависимыми во времени свойствами.

Рассмотрим мостовую конструкцию с жесткостью , погонной массой и шарнирным опиранием концов. Система несет подвижную массу , положение которой в пролете характеризуется координатой (рис. 1).

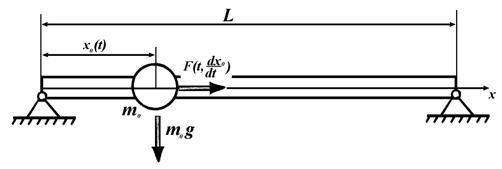
Рис. 1.Модель мостовой конструкции с подвижным инерционным включением.

Из характера силового нагружения видно, что масса перемещается под воздействием усилия , величина которого в общем случае может зависеть не только от времени , но и от скорости движения массы. В этом состоит основное отличие рассматриваемой задачи от классической постановки, где задается не движущая сила, а закон изменения скорости тела.

При построении математической модели, описывающей колебаний изображенной на рис.1 системы, будем считать, что в каждый момент времени подвижная масса разбивает пролет на два элемента с изменяемой во времени длиной - и .

Представим конструкцию конечно-элементной моделью с постоянным числом узлов дискретизации равным . Разбиение на конечные элементы проводится таким образом, чтобы первый и последний узлы совпадали с опорами моста, а один из промежуточных узлов - с положением подвижной массы. С этой целью первый участок, определяемый пройденным расстоянием инерционной нагрузки, разбивается узлами на элементы одинаковой длины . Вторая часть пролета представляется дискретной моделью с узлами. Длина конечных элементов в этом случае равна

Введем столбец координат узлов , соответствующий разбиению системы в -тый момент времени (рис.2). Здесь первые компонент соответствуют узлам первой части пролета, оставшиеся величин - узлам второго участка.

При такой расчетной схеме масса, в процессе своего движения, всегда будет находиться в точке с координатой . Следовательно, . Но так как положение массы изменяется в пределах , то для реализации предлагаемого способа дискретизации, а также для повышения точности и устойчивости численного решения, считаем, что для каждого может принимать различные значения. Эти значения будут выбираться в зависимости от заданного и величины отношения .

Пусть состояние системы упругий мост – подвижное инерционное включение в -тый момент времени описывается обобщенными координатами , описывающими линейные изгибные колебания моста и - текущим положением в пролете перемещаемой массы .

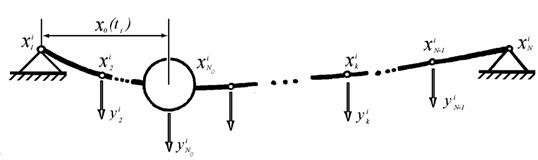
Рис. 2. Дискретная модель мостовой конструкции в -тый момент времени

Составим уравнения колебаний упругой модели и движения по ней массы в моменты времени . Для этого получим выражения кинетической и потенциальной энергий системы. Кинетическая энергия складывается из двух составляющих: энергии изгибных колебаний несущей конструкции и энергии движения дискретного включения

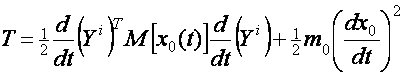(1)

Потенциальная энергия также состоит из двух частей: энергии изгиба моста, и работы сил тяжести массы при перемещении всей системы в недеформированное состояние

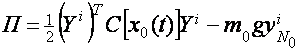(2)

В этом, выражении - прогиб точки пролета под массой .

В соотношениях (1) и (2) и - глобальные матрицы масс и жесткостей конечно-элементной модели. Как было показано ранее длины используемых конечных элементов и зависят от обобщенной координаты , а, следовательно, элементы матриц масс и жесткостей также являются фикциями положения массы , а в конечном итоге времени.

Подставляя (1) и (2) в уравнения Лагранжа второго рода и учитывая, что в качестве обобщенной силы выступает равнодействующая движущего усилия и нагрузок от сопротивления перемещению массе , получим

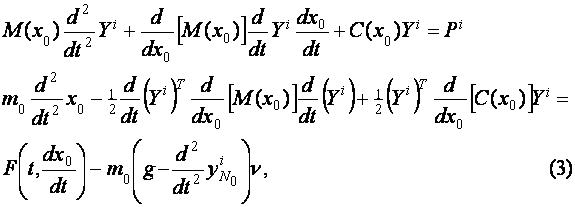
где - коэффициент сопротивления перемещению массы, - вектор-столбец нагрузок, приложенных к узлам в плоскости колебаний.

Из выражений (3) видно, что колебания упругой модели в интервале времени описываются системой нелинейных дифференциальных уравнений с переменными коэффициентами. Первая группа уравнений характеризует колебания несущей конструкции, последнее соотношение — движение массы в направлении оси под действием силы . В результате решения определяются величины , характеризующие упругие перемещения в узлах ; в момент времени . Находится и новая координата подвижной массы.

Для анализа поведения модели на следующем интервале времени ее движения , аналогично предыдущему считаем, что масса в момент разбивает всю конструкцию на два участка переменной длины: которое определяется из решения системы уравнений (3) и . Для этого шага решения вводим новые узлы дискретизации так, чтобы совпадал с с текущей координатой подвижной массы как показано на рис. 3.

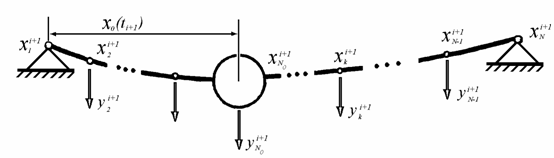
Рис. 3. Дискретная модель в -вый момент времени

Так как , то в общем и . Таким образом, для следующего шага дискретизации по времени строится расчетная схема с новым разбиением на узлы, аппроксимирующая реальную конструкцию.

Введем новые переменные - , характеризующие упругие перемещения моста для новых узлов дискретизации. Тогда уравнения движения, описывающие и колебания моста и перемещение инерционного включения, будут иметь вид, аналогичный уравнениям (3), только уже относительно новых неизвестных . В итоге решения системы дифференциальных уравнений определяются величины, характеризующие динамику системы в момент времени .

Таким образом, исследование совместных колебаний несущей упругой конструкции и подвижного инерционного включения сводится на каждом шаге дискретизации по времени к интегрированию системы дифференциальных уравнений (3). Найденные на –том шаге решения служат исходными данными для построения уравнений движения в следующий момент времени. Численная реализация такого подхода позволит анализировать не только колебательные процессы несущей упругой системы, но и характер движения инерционного включения при практически любых законах изменения усилия, вызывающего это движение.