Математика / 5. Математичне моделювання

Готинчан І.З.

Чернівецький торговельно - економічний інститут

Київського національного торговельно – економічного університету

МОДЕЛЮВАННЯ НЕСТАЦІОНАРНИХ ТЕМПЕРАТУРНИХ ПОЛІВ В НЕОДНОРІДНИХ СЕРЕДОВИЩАХ З М’ЯКИМИ МЕЖАМИ МЕТОДОМ узагальненого ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА ФУР’Є-ФУР’Є- ЛЕЖАНДРА НА декартовій ВІСІ

Нехай - одинична функція Хевісайда, - диференціальний оператор Фур’є, , - узагальнений диференціальний оператор Лежандра [3].

Розглянемо гібридний диференціальний оператор

(1)

Моделювання нестаціонарного температурного поля в кусково-однорідному середовищі за допомогою гібридного диференціального оператора математично приводить до задачі побудови обмеженого в області

розв’язку сепаратної системи диференціальних рівнянь теплопровідності параболічного типу [1]

(1)

за початковими умовами

(2)

та умовами спряження

(3)

Припустимо, що виконані умови на функції та коефіцієнти:

1) функції та є оригіналами за Лапласом стосовно [2];

2) виконані умови на коефіцієнти: .

У зображенні за Лапласом задачі (1) - (3) ставиться у відповідність задача

побудови обмеженого на множині І₂ розв'язку сепаратної системи звичайних

диференціальних рівнянь 2-го порядку [4]

(4)

за умовами спряження

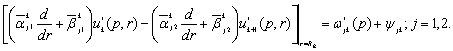(5)

У рівностях (4) - (5) прийняті позначення: , , . Зафіксуємо ту вітку, на якій

Побудову розв'язків задачі (4) - (5) проведемо методом функції Коші [4,5].

Фундаментальну систему розв'язків для рівняння утво-рюють функції та або їх лінійні комбінації та [4], а для рівняння - узагальнені приєднані функції Лежандра та [3].

Обмежений на множині І₂ розв'язок задачі (4) - (5) будемо шукати за правилами [4]:

(6)

У рівностях (6) беруть участь функції Коші [4,5]. Визначимо функції:

Безпосередньо перевіряється, що за функції Коші можна взяти функції

(7)

(8)

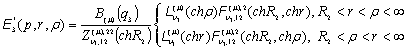(9)

Крайові умови (5) для визначення величин i дають алгебраїчну систему з чотирьох рівнянь:

(10)

У системі (10) беруть участь функції:

Визначимо функції:

Припустимо, що виконана умова однозначної розв'язності даної крайової задачі: для з де - абсциса збіжності інтеграла Лапласа, та визначник алгебраїчної системи (10):

(11)

У результаті однозначної розв'язності алгебраїчної системи (10), підстановки одержаних виразів та у формули (6) отримуємо єдиний розв'язок задачі (4) - (5):

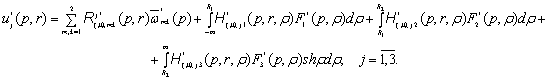( 12)

У рівностях (12) беруть участь: 1) породжені неоднорідністью системи (4) функції впливу:

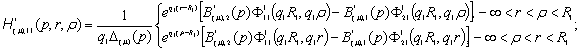
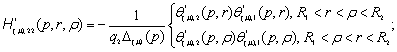(13)

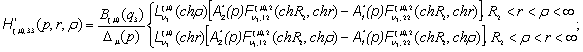
2) породжені неоднорідністю умов спряження функції Гріна:

(14)

Повертаючись в рівностях (12) до оригіналу, одержуємо єдиний розв'язок задачі теплопровідності (1) - (3:

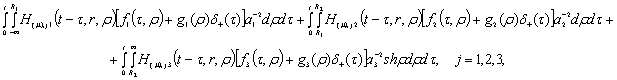(15)

дельта-функція, зосереджена в точці

Тут за означенням [5]

(16)

(17)

Особливими точками функцій Гріна та функцій впливу ) є точки галуження і . Оскільки то всі особливі точки знаходяться на лівій піввісі . Це дає можливість одержати такі структури головних розв’язків даної задачі теплопровідності:

(18)

(19)

Зауваження. Вибором параметрів, які беруть участь у формулюванні даної задачі теплопровідності, можна із загальних структур виділити безпосередньо в рамках даної моделі будь-який частковий випадок.

Література

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972. – 735с.

2. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688с.

3. Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера-Фока. – Чернівці: Прут, 2002. – 248 с.

4. Степанов В.В. Курс дифференциальных уравнений. - М.: Физматгиз, 1959. - 468 с.

5. Шилов Г.Е. Математический анализ. Второй специальный курс. - М.: Наука, 1965. - 328 с.