Івченко О.В.

Черкаський державний технологічний університет, Україна

Алгоритм оцінки параметрів негаусівських випадкових процесів за статистично залежною вибіркою методом максимізації полінома

Актуальність побудови методів і алгоритмів обробки статистичних даних на основі спостережень вимагає постійного підвищення точності вимірів (оцінювання) параметрів. Підвищення точності пов’язане з врахуванням у алгоритмах обробки всіх властивостей процесу, що спостерігається, зокрема наявності кореляції між вибірковими значеннями [1]. Метод максимізації полінома [2,3] дозволяє проводити оцінку параметрів випадкових негаусівських процесів на основі використання усереднених характеристик у вигляді моментів і кумулянтів, як данних, що описують випадковий процес.

При цьому, якщо вибіркові значення є статистично пов’язаними, то слід провести адаптацію методу максимізації полінома [4].

Нехай спостерігається вибірка об’ємом n залежних, однаково розподілених випадкових значень з випадкової величини з багатомірною функцією розподілу , де параметр є інформативним і приймає істине значення .

Згідно методу максимізації полінома [2,3] для оцінки невідомого скалярного параметра використовується узагальнений стохастичний поліном 1-го типу порядку s і розміром n виду:

, (1)

де -певні види функціонального перетворення над вибірковими значеннями.

Встановлено [6,7], що якщо у вибірковому стохастичному поліномі вигляду (1) коефіцієнти і рівні відповідно :

, , , (2)

де - математичні сподівання функцій , а функції знаходяться з вирішення системи лінійних алгебраїчних рівнянь:

, (3)

то при будь-якому кінцевому s поліном (1) асимптотично при , як функція параметра , має максимум в точці , околиці істинного значення . Причому при величина сходиться за вірогідністю до .

В вище наведених виразах:

, , .

Оцінка невідомого параметра знаходиться з рішення рівняння:

,

яке в розгорнутому вигляді для (1) дорівнює:

. (4)

У тому випадку, коли стохастичний поліном заданий в класі степеневих функцій (або описується за допомогою початкових моментів), то функції називаються центрованими корелянтами розміром і вони мають вигляд:

.

На випадок статистично залежної вибірки з досліджуваної величини, узагальнений стохастичний поліном 1-го типу порядку s і розміром n набуває вигляду:

(5)

Слід відзначити принципову відмінність полінома (5) від полінома (1), яка полягає в залежності коефіцієнтів полінома від параметрів кореляції, які представлені у вигляді матриці кореляції Z:

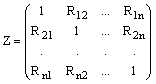, (6)

де - коефіцієнти кореляції, які характеризують степінь зв’язку між вибірковими значеннями і можуть бути визначенні як стандартні функції кореляції, що часто використовуються на практиці [3].

При цьому коефіцієнти полінома (5) і рівні відповідно:

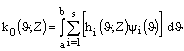,. (7)

Показано, що для статистично залежних випадкових величин оцінка невідомого параметра буде знаходиться з рішення стохастичного рівняння наступного виду:

, (8)

яке визначається як похідна по шуканому параметру від стохастичного поліному виду (5).

Функції в цьому випадку знаходяться з вирішення системи лінійних алгебраїчних рівнянь:

, , (9)

де для випадкової величини з статистичним зв’язком першого порядку корелянти і центровані корелянти виражаються через одномірні і сумісні моменти наступним чином:

,, (10)

де - прості одномірні моменти рядку і,

- сумісні моменти порядку .

Коефіцієнти , що знаходяться з рішення рівняння (9) для випадкових величин з статистичним зв’язком першого порядку також визначаються через кореляційні функції, як міри зв’язку між вибірковими значеннями.

Таким чином відбувається перехід від одномірних моментів, які характерні для одномірних розподілів, до багатомірних моментів, як характеристик багатомірного характеру досліджуваної величини.

Показано, що оцінки невідомого параметра знайдені з рішення рівняння (8) будуть ефективними і асимптотично незміщеними.

В роботі [5] показано, що для полінома з коефіцієнтами , що знайдені з рішення системи лінійних алгебраїчних рівнянь (3), справедлива наступна рівність:

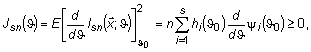(11)

де функція - кількість добутої інформації про параметр з незалежної вибірки об'ємом n методом максимізації полінома.

Показано, що кількість добутої інформації прямо пропорційна об'єму вибірки n:

,

де називається кількістю добутої інформації з одного вибіркового значення.

Слід відзначити, що кількість добутої інформації в загальному випадку менша кількості інформації Фішера , хоча в певних випадках спостерігається їх рівність.

Для статистично залежної випадкової величини кількість добутої інформації залежить від параметрів кореляції, які визначають коефіцієнти полінома. Тому математичний вираз для визначення кількості добутої інформації з корельованої випадкової величини методом максимізації полінома має вигляд:

(12)

З виразів (11) і (12) видно, що кількість добутої інформації залежить від вибору функцій .

Для функцій (4) дисперсія оцінки, що знайдена методом максимізації полінома, буде асимптотично рівна:

.

Як показано [5,6], якщо в рівнянні (1) з функціями , узяти (s+1) член, то для оцінки, знайденої методом максимізації полінома, асимптотично справедлива наступна нерівність:

, або ,

де - асимптотична дисперсія оцінки, коли кількість членів в поліномі (1) рівна s.

Закономірність збільшення кількості добутої інформації з ростом степеня стохастичного полінома зберігається і на випадок статистично залежної випадкової величини. Але слід відзначити, що в випадку кореляційного статистичного зв’язку дисперсія, як обернена функція до кількості добутої інформації, може змінюватись за рахунок кореляційних функцій, які визначають значення коефіцієнтів полінома (9).. Тобто представляє інтерес дослідження поведінки дисперсії шуканої оцінки для різних видів функцій кореляції [8].

Література

1. Малахов А.Н. Кумулянтный анализ случайных негауссовых процессов и их преобразование. М.”Сов. радио”, 1978.-376с.

2. Кунченко Ю.П. Стохастические полиномы.-К.: Наук. Думка, 2006.-275с.