Д.э.н. Стрельцова Е.Д., К.т.н. Стрельцов В.С.

Вероятностные автоматы как средство моделирования пропорций распределения налогов

Южно-Российский государственный технический университет (НПИ), Россия

Авторами излагается автоматный подход к созданию математической модели долевого распределения налогов между уровнями бюджетной системы. Стохастический автомат представляет собой абстрактное адаптивное управляющее устройство, находящееся в каждый момент времени в одном из возможных состояний и способное переходить из состояния , , в состояние . Состояния автомата определяются следующим образом. Отрезок [0;1] разбивается на конечное число отрезков, равное . Координаты концов этих отрезков принимаются в качестве состояний автомата , где , , , …, . Выбирая состояния , , интерпретируемые как величины долей отчислений денежных средств от уплаты налогов в порядке бюджетного регулирования, автомат вызывает изменение остатков денежных средств в бюджете нижестоящего уровня бюджетной системы РФ до некоторой величины . Величина принимается в качестве выходов (или воздействий) автомата в момент времени . Автомат рассматривается функционирующим во внешней случайной среде, которая реагирует на выходы автомата следующим образом. Множество реакций внешней среды разбито на два класса: благоприятные и неблагоприятные реакции. Выход автомата вызывает благоприятную реакцию у внешней случайной среды, если в бюджете в момент времени образовался текущий профицит, т.е. если . Поощрение автомата идентифицируется поступлением на его вход в момент времени входного сигнала , означающего «выигрыш». Неблагоприятная реакция внешней случайной среды возникает при образовании в бюджете в момент времени текущего дефиците, т.е. . В этом случае автомат штрафуется и на его вход поступает сигнал , означающий «штраф» или «проигрыш». Обозначим вероятность выигрыша автомата в состоянии , , через . Тогда вероятность проигрыша автомата в состоянии составит . Вектор рассматривается как вероятностные характеристики внешней случайной среды, в которую погружён автомат . Авторами предложена структура автомата , в соответствии с которой ему предписывается следующее поведение. Если автомат в момент времени находился в состоянии и в этот момент выиграл (т.е. в момент на его вход поступил сигнал ), то в момент времени он остаётся в этом же состоянии. Если же автомат в момент времени находился в состоянии и в этот момент проиграл (т.е. в момент на его вход поступил сигнал ), то в момент времени он перейдёт в любое другое состояние . Вероятность перехода автомата из состояния в состояние одинакова для любого и равна . Матрицы перехода автомата из состояния в состояние при выигрыше и при проигрыше имеют вид:

; .

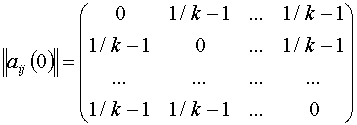Вероятности перехода автомата из состояния в состояние при любом входном сигнале определяются исходя из выражения . В соответствии с этим выражением матрица перехода автомата из состояния в состояние , запишется следующим образом:

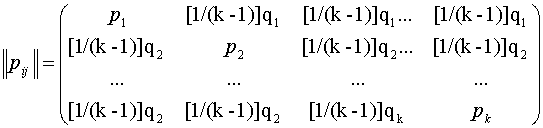
Финальные вероятности пребывания автомата в состоянии обозначим . Тогда , где транспонированная матрица, имеем следующую систему уравнений для определения финальных вероятностей :

.

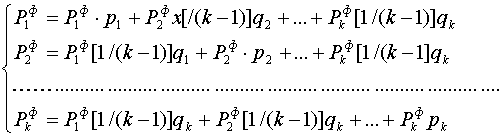Используя эту систему уравнений, а так же условие нормировки 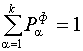, получены выражения для финальных вероятностей пребывания автомата в состоянии : ; ; …; . Состояния автомата , рассматриваются в качестве возможных решений относительно величины нормативов отчислений финансовых ресурсов в бюджеты муниципальных образований от уплаты налогов и сборов, подлежащих зачислению в бюджет регионального уровня бюджетной системы РФ. Финальные вероятности дают количественную оценку целесообразности принятия этих решений.

Выводы.

В результате проведённых исследований получены следующие результаты, отличающиеся научной новизной:

1. Предложена адаптивная автоматная модель принятия решений относительно пропорций распределения федеральных и региональных налогов и сборов в структуре <регион>↔<муниципальное образование>, отличающаяся способностью хорошо приспосабливаться к изменениям доходов и расходов бюджета.

2. Разработана структура стохастического автомата, функционирующего в случайных средах, положенная в основу модели бюджетного регулирования и отличающаяся возможностью перехода автомата не только в соседние состояния, но и в любые другие состояния. Преимущество такой структуры состоит в возможности использования дифференцированного подхода к исследованиям по выбору пропорций распределения налоговых доходов каждого вида.

3. Выведены формальные выражения для финальных вероятностей выбора автоматом конкретного состояния, отражающего величину нормативов отчислений финансовых ресурсов от уплаты налогов порядке бюджетного регулирования. Полученные выражения позволяют дать количественную оценку возможным решениям, принимаемым при долевом распределении налоговых доходов между уровнями бюджетной системы.

Литература:

1. Системы поддержки принятия решений при управлении процессами бюджетного регулирования: Модели, методы, технологии [Текст]: Монография / Е.Д. Стрельцова; Федеральное агенство по образованию, Юж-Рос. гос. техн. ун-т.–Новочеркасск: ЮРГТУ; ООО НПО «ТЕМП», 2005.– 180 с. - 11,6 п.л.)