Економічні науки/ 8. Математичні методи в економіці

Гнатчук І.Я., Федосюк С.В.

Буковинська державна фінансова академія, Україна

Модель ринку із запізненням реалізації

Дуже часто виникає така ринкова ситуація, що цикл виробництва продукції відстає від циклу її реалізації. Це характерно, наприклад, для сільського господарства. І в промисловому виробництві пропозиція формується на основі ціни в попередній період. Таким чином, функція пропозиції зміщена за часом відносно ціни , тобто будемо вважати, що , в той час, коли функція попиту одномоментно відповідає ціні: . Розглянемо простіший випадок, коли попит і пропозиція лінійно залежать від ціни:

, , . (1)

Умова рівноваги передбачає рівність передбачуваного і затребуваного объемів товарау: , звідки з врахуванням (1) маємо

або

Поділивши обидві частини цієї рівності на і перейшовши для зручності на крок вперед по часу, отримаємо лінійне неоднорідне різницеве рівняння першого порядку [1] відносно ціни з постійними коефіцієнтами:

(2)

Нехай тоді

Характеристичне рівняння має єдиний корінь рівний . Частинний же розв’язок рівняння (2) зручно шукати у вигляді постійної величини:

.

Після підстановки останніх співвідношень у рівняння (2) частинний розв’язок легко визначається:

(3)

Величина є рівноважною ціною [4]. Загальний розв’язок рівняння (2) визначається формулою [3]

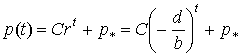, (4)

де С − довільна стала.

Нехай в початковий момент часу відома ціна (задача Коші [3]), тоді підстановкою у рівняння (4) знаходимо

або .

Остаточно отримуємо

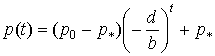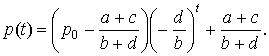або (5)

Проаналізуємо отриманий розв’язок. В залежності від вхідних параметрів задачі і формул (1) динаміка ціни в часі може бути різною. Тут можливі три варіанти [2]:

1) − поточна ціна розбігається з рівноважною ціною зі збільшенням розмаху коливань навколо неї;

2) − поточна ціна прямує до рівноважної ціни з коливаннями в її околі;

3) − дві точки рівноваги: в залежності від парності t має місце коливання від однієї точки до іншої.

Література

1. Солодовников А.С., Бабайцев В.А., Браилов В.А.. Математика в экономике − М: Финансы и статистика, 1999. – 425 с.

2. Красс М.С. Математика для экономических специальностей – М.: ИНФРА - М., 1999. – 345 с.

3. Математика в экономике: Учебно-методическое пособие// под редакцией Н. Ш. Кремера – М: Финстатинформ, 1999. – 455 с.

4. Барковський В.В.,Барковська Н.В. Вища математика для економістів.−

К.:ЦУЛ, 2002. – С.274-278.