Каганская Ю.В., Алексеев М.А.
Национальный
горный университет, Украина
Перестраиваемые спектральные
операторы для формирования информативных признаков сигналов управления роторных
объектов
Введение. Современная экономическая ситуация в Украине не дает возможности значительной
части предприятий приобретать оборудование и поэтому актуальным становится
вопрос о том, каким образом можно дольше и эффективнее использовать имеющееся
оборудование. Надежный контроль параметров и диагностирование технического
состояния объектов управления представляет интерес, как с научной, так и с
практической точки зрения.
Особый интерес представляют методы
неразрушающего контроля, например, вибродиагностика, задачей которой является контроль
параметров объекта на основе анализа вибрационных
сигналов, сопровождающих функционирование объекта.
При решении задач контроля и диагностики с
помощью существующих методов возникают определенные трудности при распознавании
состояния объекта, определения причин, вызывающих отклонение параметров и
появление неисправностей. Это обусловлено тем, что функционирование объектов
разных типов сопровождается процессами различной физической природы. Использование
для контроля параметров методов, не учитывающих особенности этих процессов, не
позволяет формировать информативные признаки диагностических сигналов. Поэтому
возникает необходимость создания методов анализа диагностических сигналов,
позволяющих получить более точное определение параметров объектов управления.
Анализ существующих достижений и публикаций.
Среди широко используемых методов выделения информативных признаков следует выделить основанные на применении ортогональных преобразований, особенно те из них, которые обладают быстрыми вычислительными алгоритмами. Ортогональные преобразования при соответствующем выборе базисной системы обеспечивают адекватность анализируемой информации при высокой степени декорреляции информативных компонент. Характер изменения коэффициентов позволяет получить информацию об объекте управления. Важнейшим свойством спектра Фурье является возможность оценки глобальных свойств сигналов, его инвариантность к временному сдвигу.
Основным недостатком
Фурье-преобразования является его "глобальная" чувствительность к
"локальным" скачкам и пикам функции. При этом модификация коэффициентов Фурье
(например, подавление высоких гармоник с целью фильтрации шума) вносит
одинаковые изменения в поведение сигнала на всей области определения. Это
особенность оказывается полезной для стационарных сигналов, свойства которых в
целом мало меняются со временем. При исследовании нестационарных сигналов
требуется использование некоторых локализованных во времени компактных волн,
коэффициенты разложения по которым сохраняют информацию о дрейфе параметров
аппроксимируемой функции. Попытки построения таких систем функций сводились к
сегментированию сигнала на фрагменты ("окна") с применением
разложения Фурье для этих фрагментов .
Однако оконные преобразования
позволяют проанализировать либо высокие частоты в коротком окне времени, либо
низкочастотную компоненту, но не оба колебания одновременно. В результате был
предложен подход, в котором для различных диапазонов частот использовались временные
окна различной длительности. Оконные функции получались в результате
растяжения-сжатия и смещения по времени какой-либо одной базисной функции. Эти базисные функции называются вейвлетами (wavelets)
- компактными волнами.
Вейвлет-преобразования
отличаются высокой степенью локализованности базисных функций как во
временной, так и в частотной областях, что позволяет применять их для обработки
широкого класса процессов, в том числе и нестационарных. Однако построение
новых систем базисных вейвлет-функций представляет собой достаточно сложную
проблему. Выбор того или иного класса анализирующих функций диктуется спецификой
задачи, тем, какую информацию нужно извлечь из сигнала.
При решении задач оперативного контроля параметров объектов управления
реализация вейвлет-преобразования сдерживается значительным объемом вычислений и,
как следствие, низкой скоростью обработки данных. Частично эта проблема
решается разработанными методами быстрых преобразований. Однако эти методы не
всегда пригодны для анализа произвольных сигналов, что способствует поиску
новых подходов снижения вычислительных затрат.
Выбор того или иного метода преобразования сигналов зависит от
поставленной задачи и типа имеющихся данных, которые необходимо обработать, от
возможностей вычислительной техники и от того, в каком виде необходимо
представить результат.
Формулировка цели и задачи исследований
Целью работы является разработка математического аппарата, позволяющего
синтезировать вейвлетоподобные ортогональные системы базисных функций
субоптимальных по Карунену-Лоэву, учитывающих особенности анализируемых сигналов и обладающих возможностью
параметрического перестраивания.
Изложение основного материала исследований
В работе [1]
рассматривается метод формирования обобщенных спектральных ядер перестраиваемого
спектрального оператора, представляемого в матричной форме. Метод позволяет
получать новые базисы как одноядерные, так и многоядерные, обладающие
свойствами ортогональности и полноты, имеющие алгоритмы быстрых преобразований.
Используемое понятие ортогональных базисных систем и ядра спектрального
оператора рассматривается в рамках теории линейных дискретных преобразований. В
работе [2] предложен метод формирования субоптимальных по Карунену-Лоэву
перестраиваемых спектральных операторов для контроля параметров объектов
управления.
Операция
нахождения дискретного спектра ![]() цифровыми методами
может быть представлена в виде матричного произведения
цифровыми методами
может быть представлена в виде матричного произведения
|
|
(1) |
где ![]() - вектор анализируемой реализации
размерностью
- вектор анализируемой реализации
размерностью ![]() ,
, ![]() ,
,
![]() - квадратная матрица
спектрального оператора размерностью
- квадратная матрица
спектрального оператора размерностью ![]() .
.
Число строк
матрицы спектрального оператора ![]() равно количеству
базисных функций, участвующих в разложении, а элементы строки представляют
собой дискретные значения одной из базисных функций в моменты дискретизации.
равно количеству
базисных функций, участвующих в разложении, а элементы строки представляют
собой дискретные значения одной из базисных функций в моменты дискретизации.
Непосредственное
вычисление дискретного спектра ![]() по (1) требует
по (1) требует ![]() операций типа
умножение-сложение. Эффективным средством сокращения количества вычислений
дискретного спектра являются алгоритмы быстрых преобразований, математической
базой которых послужил метод матричной факторизации Гуда [1], суть которого
состоит в устранении избыточности матрицы спектрального оператора, обладающего
свойствами ортогональности и полноты, за счет представления ее в
факторизованном виде
операций типа
умножение-сложение. Эффективным средством сокращения количества вычислений
дискретного спектра являются алгоритмы быстрых преобразований, математической
базой которых послужил метод матричной факторизации Гуда [1], суть которого
состоит в устранении избыточности матрицы спектрального оператора, обладающего
свойствами ортогональности и полноты, за счет представления ее в
факторизованном виде
|
|
(2) |
где ![]() - разреженная нулями
и далее неразложимая матрица.
- разреженная нулями
и далее неразложимая матрица.
Ненулевые
столбцы одной зоны образовали квадратную матрицу размерностью ![]() , которую Гуд назвал обобщенным спектральным ядром:
, которую Гуд назвал обобщенным спектральным ядром:
|
|
(3) |
где ![]() - порядковый номер
ядра (
- порядковый номер
ядра ( ![]() );
); ![]() - номер простого
множителя
- номер простого
множителя ![]() в представлении
в представлении 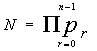 ,
, ![]() ;
; ![]() - размер матрицы
спектрального оператора
- размер матрицы
спектрального оператора ![]() ;
; ![]() - индексы
соответственно строки и столбца (
- индексы
соответственно строки и столбца ( ![]() ).
).
Особенностью
ядра является независимость его размеров от количества синтезируемых базисных
функций. Однако число ядер, необходимых для формирования спектрального
оператора, определяется как количеством базисных функций, так и основанием
выбранной системы счисления, то есть ![]() . Элементы всех ядер могут отличаться друг от друга или быть
одинаковыми. Примером многоядерной системы является базис Фурье, одноядерной
системы - базис Уолша.
. Элементы всех ядер могут отличаться друг от друга или быть
одинаковыми. Примером многоядерной системы является базис Фурье, одноядерной
системы - базис Уолша.
Благодаря
разреженной структуре матриц Гуда произведение любых двух матриц ![]() будет давать в
результате матрицу, ненулевые элементы которой составляются только из
произведений двух членов.
будет давать в
результате матрицу, ненулевые элементы которой составляются только из
произведений двух членов.
В [1]
изложен подход к формированию приспособленных матричных спектральных
операторов, основанный на их представлении через обобщенное спектральное ядро (
![]() ), что позволяет
получить бесчисленное множество базисных систем функций с алгоритмами быстрых
преобразований.
), что позволяет
получить бесчисленное множество базисных систем функций с алгоритмами быстрых
преобразований.
В основе
матрично-ядерного представления спектрального оператора для
р = 2 лежит возможность синтеза
базиса из элементарных микроструктур-ядер, обобщенная форма которых имеет вид:
|
|
(4) |
|
|
где |
|
|
Углы
параметры ![]() и
и ![]() являются степенями свободы
ядра и определяют конкретные элементы спектрального оператора.
являются степенями свободы
ядра и определяют конкретные элементы спектрального оператора.
Например,
системе дискретных экспоненциальных функций Фурье соответствуют углы-параметры 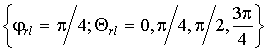 , базису Уолша
, базису Уолша ![]() , базису Хаара
, базису Хаара ![]() .
.
Достоинством
одноядерных базисов является простота формирования их функций, в частности
функций Уолша. Однако ограниченное число степеней свободы не позволяет в
некоторых задачах выполнять корректировку или параметрическую перестройку ряда
функций базисной системы. Однопараметрическое семейство базисных систем с
ядрами вида
|
|
(5) |
позволяет
формировать известный базис Уолша. Например, ядро базиса Уолша-Адамара имеет
вид
|
|
(6) |
В
большинстве случаев более целесообразным является использование многоядерных
базисов с ядрами
|
|
(7) |
Многоядерные
базисы обладают значительными возможностями в отношении перестройки как
отдельных функций (строк или столбцов матрицы-оператора), так и всего базиса в
целом. Например, базис Хаара для любого размера формируется из ядер двух типов
|
|
(8) |
Концепция
ядерного представления спектральных операторов не только упрощает процедуру их
синтеза, но и позволяет производить обоснованный по комплексу критериев выбор
базиса.
Следует отметить, что в
отличие от известных алгоритмов быстрых преобразований в традиционных базисах,
позволяющих вычислять спектральные коэффициенты только в одном базисе, алгоритм
быстрого преобразования в приспособленных базисах является унифицированным, так
как зависит от расположения ядер, определяемых углами [1].
Выражения
для углов-параметров при N=8 имеют вид [1]:
|
|
(9) |
где ![]() - компоненты эталона
- компоненты эталона ![]() .
.
В общем
случае при ![]() справедливы следующие
соотношения для углов-параметров, образующих ядра спектрального оператора [1]:
справедливы следующие
соотношения для углов-параметров, образующих ядра спектрального оператора [1]:
|
|
(10) |
У части ядер
параметры не зависят от исходного эталона (это ядра с углами φ12,
φ13, φ14, φ23, φ24). Эти ядра
определяют оставшиеся N(n/2-1)+1 степеней свободы и позволяют провести
дальнейшую оптимизацию базиса под требование конкретной задачи сжатия,
например, уменьшения памяти вычислительных средств, времени вычисления,
упрощения вида базисных функций, приспособление к известному закону
распределения обрабатываемых сигналов. Например, если отклонения от эталона
носят равновероятный характер, то нет необходимости использования оставшихся
степеней свободы в ядрах спектрального оператора. Это означает, что достаточно
обеспечить выполнение следующих условий, накладываемых на углы спектрального
оператора (базис 1 типа, рис.1а):
|
|
(11) |
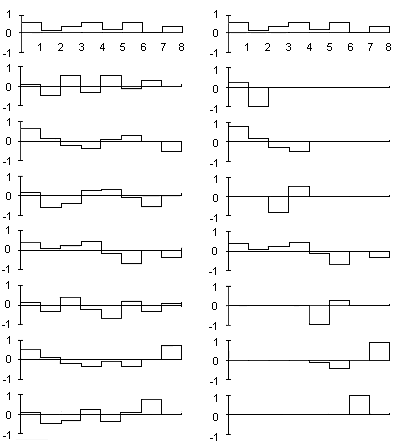
а) б)
Рис.1. Функции перестраиваемых
спектральных операторов 1 типа (а) и
2 типа - вейвлетоподобных (б)
При
использовании такой закономерности расстановки углов-параметров в случае
необходимости уточнения разложения при увеличении размерности в два раза
исходного вектора. При этом ранее вычисленные значения углов-параметров
остаются без изменения, и расчет новых углов выполняется только для добавляемых
матриц.
Рассмотрим
другой случай, когда отклонение от эталона носит сосредоточенный во времени
характер. В этом случае целесообразно построить такой базис, функции которого
отличаются локальным поведением на интервале определения и равны нулю на
большей его части (подобно базису Хаара). Свойство наилучшего равномерного
приближения, свойственное базису Хаара, можно придать и базису, построенному по
методике приспособления к эталону. Для этого необходимо положить оставшиеся
углы-параметры равными нулю, то есть добавить только одну степень свободы (перестраиваемый
спектральный оператор 2 типа
(вейвлетоподобных, рис. 1б))
|
|
(12) |
Выводы
Предложенный
подход с использованием перестраиваемых субоптимальных по Карунену-Лоэву
базисов позволяет выбрать построить базисы, учитывающие как глобальные свойства
анализируемого сигнала на всем интервале определения (базис 1 типа), так и
вейвлетоподобные базисы, которые учитывают локальные изменения сигнала подобно
базису Хаара (вейвлетам Хаара). Это позволяет в рамках единого подхода
совместить преимущества спектрального анализа и вейвлет-анализа сигналов при
опретивном контроле параметров объектов управления.
2. Продолжение исследований
целесообразно проводить в направлении разработки математических методов синтеза дискретных параметрически
перестраиваемых ортогональных вейвлет-функций.
Список литературы
1.
Солодовников А.И. Основы
теории и методы спектральной обработки информации [Текст]: учеб. пособие / А.И.
Солодовников, А.М. Спиваковский. – Л.: Изд-во Ленингр. ун-та, 1986. – 272 с.
2. Алексеев М.А. Метод формирования параметров для
ситуационного управления технологическими
процессами // Сб.научн.тр. НГУ № 27. - Днепропетровск.- 2007, С.152-156.
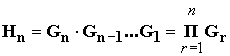
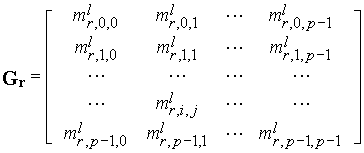
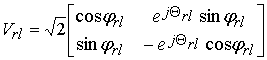
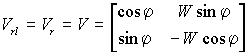
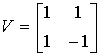
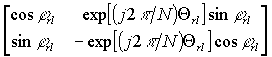
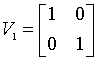
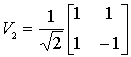
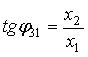
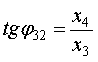 ;
; 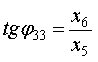
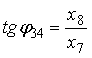
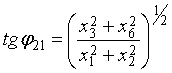 ;
; 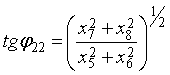 ;
;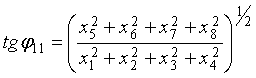
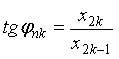 ;
; 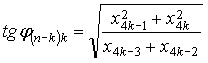 ;
; 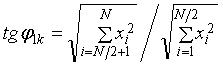 .
.