к.т.н. Сікора О. В., Берегуляк Л.В., Остапчук Л.А.

Дрогобицький державний педагогічний університет ім. І. Франка, Україна

ВИЗНАЧЕННЯ нестаціонарного температурного поля в безмежній пластинці з прямокутним вирізом

Розглянемо однорідну необмежену пластинку товщиною в системі координат з прямокутним вирізом , . Через бокові поверхні пластинки і прямокутну границю вирізу здійснюється теплообмін з оточуючим середовищем за законом Ньютона. Нехай температура середовища, яке омиває поверхні , рівна нулю, а на прямокутних границях вирізу задано температуру . Крім того припускаємо, що на безмежності температура пластинки та її градієнти у відповідних напрямах прямують до нуля. Поставимо задачу визначення температурного поля в розглядуваній системі.

Для визначення нестаціонарного температурного поля маємо таку крайову задачу [1]

, (1)

при , (2)

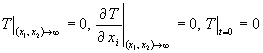, (3)

де в рівнянні (1) та крайових умовах (2), (3) позначено: ; – коефіцієнт температуропровідності; – коефіцієнт теплопровідності; – час; – коефіцієнт тепловіддачі з поверхонь ; – характеристична функція відрізка; – одиничні функції Гевісайда.

Для узагальненої функції , , враховуючи умову (2), а також правила диференціювання узагальнених функцій, маємо таке диференціальне рівняння

. (4)

Фундаментальний розв’язок рівняння (4), який відповідає миттєвому точковому джерелу тепла одиничної інтенсивності має вигляд

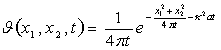. (5)

Оскільки права частина рівняння (4) фінітна, то його розв’язок можна одержати у вигляді згортки фундаментального розв’язку (5) і правої частини рівняння (4), тобто

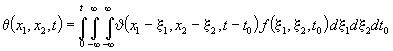, (6)

де

.

Врахувавши вид функції , маємо залежність

. (7)

Обчислюючи інтеграли у правій частині рівності (6), беручи при цьому до уваги залежність (7), дістанемо таке інтегральне представлення для узагальненої функції :

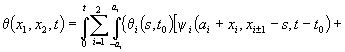
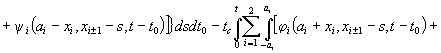
. (8)

У виразі (8) введено такі позначення для ядер в інтегралах:

; ; .

Ядра під інтегралами у поданні (8) визначені для всі значень координат та для величин часу не рівному значенню . Неважко переконатись, що їх можна довизначити за неперервністю також і для , тобто для всіх значень аргументів. Для цього розглянемо таку функцію

.

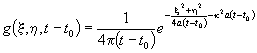Виконуючи заміну будемо мати і при ; звідси після граничного переходу дістаємо

.

Отже, в інтегральному представленні (8) можна здійснювати граничний перехід по всіх аргументах. Покладаючи тоді у (8) приходимо до такої системи інтегральних рівнянь для визначення невідомих значень , функції :

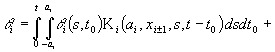
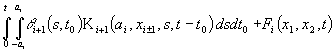.(9)

Тут позначено:

;

;

.

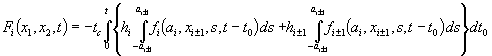Отримані інтегральні рівняння (9) належать до Вольтерового типу за часом і до Фредгольмовому по геометричних координатах ; їх розв’язок може бути знайденим методом послідовних наближень .

Література:

1. Подстригач Я. С. Температурные поля и напряжения в элементах электровакуумных приборов / Я. С. Подстригач, Ю. М. Коляно, М. М. Семерак. - М. : Наука, 1981. - 344 с.

2. Подстригач Я.С. Термоупругость тел неоднородной структуры / Я. С. Подстригач, В. А. Ломакин, Ю. М. Коляно. - М. : Наука, 1984. - 378 с.