К.ф.-м.н. Дорошенко М.В., Когут У.П., Коваль Г.П.

Дрогобицький державний педагогiчний унiверситет iменi Iвана Франка, Україна

Чисельне розв'язування двовимірних інтегральних рівнянь Фредгольма першого роду зі слабкою особливістю в ядрі

До розв'язування крайових задач для рівнянь еліптичного типу зводиться моделювання багатьох практичних задач, наприклад, розрахунку електростатичних полів, які створюють електронно-оптичні системи. Така задача зводиться до розв'язування просторової внутрішньої або зовнішньої задачі Діріхле для рівняння Лапласа.

Ефективним методом розв'язування крайових задач для рівнянь еліптичного типу є метод інтегральних рівнянь. Метод інтегральних рівнянь застосовувався для розв'язування задачі Діріхле для рівняння Лапласа в роботах [1-3]. За допомогою данного методу розв'язування зовнішньої та внутрішньої задач Діріхле для рівняння Лапласа зводиться до розв'язування інтегральних рівнянь Фредгольма першого роду зі слабкою особливістю в ядрі. Ефективність методу інтегральних рівнянь полягає в тому, що розмірність задачі зменшується на одиницю.

В даній роботі пропонується чисельний алгоритм розв'язування просторових крайових задач Діріхле для рівняння Лапласа, який зводиться до розв'язування двовимірних інтегральних рівнянь Фредгольма першого роду зі слабкою особливістю в ядрі методом колокації з використанням кубічних ізопараметричних граничних елементів для апроксимації невідомої густини та граничних поверхонь.

Просторову крайову задачу Діріхле для рівняння Лапласа [1,2] можна звести до розв'язування такого двовимірного інтегрального рівняння Фредгольма першого роду

, (1)

де S – гранична поверхня,

Для чисельне розв’язування інтегрального рівняння (1) використовувався метод колокації, а для апроксимації невідомої густини та граничної поверхоні кубічні ізопараметричні граничні елементи [2].

Граничну поверхню апроксимуємо за допомогою дванадцятивузлових ізопараметричних граничних елементів. Тоді декартові координати довільної точки елемента , на які розбивається гранична поверхня, представляються через координати вузлових точок та деякі функції від внутрішніх координат таким чином, а саме:

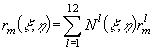, (2)

де; ;

Отже, представлення (2) забезпечує відображення кожного елементу в одиничний квадрат D = [-1,1]*[-1,1]. Невідому густину в рівнянні (1) представимо у вигляді

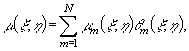(3)

де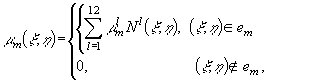

– значення невідомої густини в l – тому вузлі елементу ; функції - функції, які враховують особливості густини на краю розімкнутої поверхні [1,3].

Враховуючи (2),(3) інтегральне рівняння (1) набуде вигляду

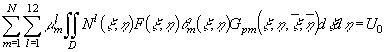, (4)

де ; ;

;

Невідомі коефіцієнти визначаємо із системи лінійних алгебраїчних рівнянь, яку отримаємо з рівняння (4) метод колокації.

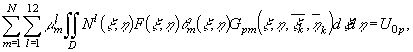(5)

де - точки колокації.

Коефіцієнти отриманої системи лінійних алгебраїчних рівнянь (5) мають сингулярну особливість на краях розімкнутих поверхонь, а ядро – слабку особливість при суміщенні точки спостереження з точкою інтегрування. Якщо поверхні замкнуті, то отримані коефіцієнти мають тільки слабку особливість.

Особливості на краю розімкнутих поверхонь виділяються заміною змінних [1]. Слабка особливість в ядрі виділяється за методикою ослаблення особливостей Канторовича [1], тобто, від підінтегральної функції віднімається та додається функція, яка поводить себе в особливій точці як підінтегральна функція, а інтеграл від неї знаходиться аналітично.

Література:

1. Бакалец В.А., Людкевич И.В. Численное решение пространственных задач электронной оптики методом интегральных уравнений. Учебное пособие. – Львов: Изд-во ЛГУ, 1986. – 135с.

2. Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. – М.: Наука, 1984. – 475с.

3. Ильин В.П. Чисельные методы решения задач электрофизики. – М.: Наука, 1986. – 395c.