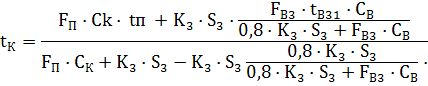ст.викл. ЖУРАКОВСЬКИЙ Я. Ю., cтудент ШУХ Б. І.

Національний технічний університет України «Київський політехнічний інститут», Україна

Математичне моделювання статики та динаміки холодильника дистиляту

Холодильник дистиляту – кожухотрубний теплообмінник в якому відбувається охолодження дистиляту, що надходить із подільника флегми. Холодильник може використовуватись в багатьох технологічних процесах, де присутня дистиляція води, наприклад, в процесі очищення стічної води методом ректифікації.

Метою дослідження є розробка математичної моделі динаміки та статики холодильника дистиляту на основі фізичних законів, за якими відбувається процес теплообміну в апараті.

Розрахункову схему холодильника з позначенням основних технологічних параметрів наведено на рисунку 1.1. На цій схемі позначені такі технологічні параметри:

F_П – витрата дистиляту, який надходить із подільника флегми до холодильника;

t_п, t_К, C_п, C_К – температура та теплоємність дистиляту (вихідної речовини) на виході з теплообмінника;

F_В3, C_В – витрата та теплоємність води що охолоджує дистилят;

t_В31 – температура води на вході в теплообмінник;

t_В32 – температура води на виході із теплообмінника.

При моделюванні статичного режиму холодильника дистиляту робимо такі припущення:

1. об’єкт розглядається як об’єкт із зосередженими параметрами;

2. витрата дистиляту на вході в теплообмінник не змінюється з часом;

3. теплоємність дистиляту і води зі зміною температури залишається сталою;

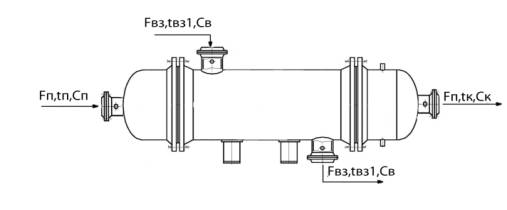
Рисунок 1.1 – Розрахункова схема холодильника дистиляту

Оскільки необхідно регулювати температуру дистиляту на виході з холодильника за допомогою охолоджуючої води, що подається в його міжтрубний простір, розглядаємо такі входи та виходи:

· вихід – температура дистиляту на виході (t_К);

· вхід – витрата води у теплообміннику (F_В3);

· збурення – температура води для охолодження дистиляту (t_В31) та витрата дистиляту (F_П).

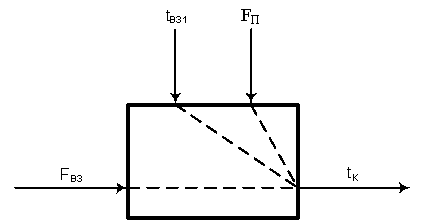
Рисунок 1.2 – Структурно-параметрична схема холодильника дистиляту

Тепловий баланс трубного простору [1]:

Q_П – Q_К – Q_ТОБ3 = 0,

де Q_П = F_П·C_k·t_п – кількість тепла, яке приноситься дистилятом;

Q_К = F_П·C_К·t_К – кількість тепла, яке виносить дистилят;

Q_ТОБ3 = K₃·S₃·( t_К – t_В32) – кількість тепла теплообміну, яке відбирається водою в міжтрубному просторі. Тут К₃ – коефіцієнт теплопередачі, S₃ – площа поверхні теплообміну.

Тепловий баланс води в міжтрубному просторі:

Q_В31 + Q_ТОБ3 – Q_В32 – Q_НС3= 0,

де Q_В31=F_В3·t_В31·C_В – кількість тепла, принесеного потоком води у між трубний простір холодильника;

Q_В32=F_В3·t_В32·C_В – кількість тепла, винесеного потоком води з міжтрубного простору холодильника;

Q_НС3=0,2·Q_ТОБ3 – кількість тепла, яке втрачається з міжтрубного простору холодильника в навколишнє середовище.

Зміна вихідної температури дистиляту описується рівнянням, що складає статичну модель процесу:

(1)

При моделюванні динамічного режиму використовуються такі додаткові технологічні параметри, а саме:

· об’єм дистиляту в трубному просторі холодильника - V_Д,

· об’єм води в міжтрубному просторі холодильника - V_В,

· площа теплообміну в холодильнику – S.

Позначимо коефіцієнт теплопередачі від дистиляту в холодильнику до охолоджуючої води як α.

Рівняння динаміки для трубного простору [2]:

F_П· t_п·C_п – F_П·t_К·C_К – α·S·( t_К – t_В32) = C_К·V_Д·ρ_К·,

де V_Д – об’єм дистиляту в трубному просторі теплообмінника;

ρ_К – густина дистиляту.

Рівняння динаміки для міжтрубного простору:

F_В3·t_В31·C_В + 0,8·α·S·( t_К – t_В32) – F_В3·t_В32·C_В = C_В·V_В·ρ_В·,

де V_В – об’єм води в міжтрубному просторі теплообмінника;

ρ_В – густина води.

Після лінеаризації, перетворення за Лапласом та всіх необхідних спрощень отримаємо рівняння, яке приведене до канонічної форми:

CК·VД·ρК·CВ·VВ·ρВ	·p^2·tК(p)+
(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) – 0,8·α^2·S^2

+	CК·VД·ρК·( FВ3·CВ + 0,8·α·S)+ (FП·CК+α·S)·CВ·VВ·ρВ	·p·tК(p)+tК(p)=
	(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) – 0,8·α^2·S^2

=	α·S·( tВ31·CВ – tВ32·CВ)	·FВ3(p).
	(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) -0,8·α^2·S^2

Введемо позначення:

A1 =	CК·VД·ρК·CВ·VВ·ρВ	,
	(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) – 0,8·α^2·S^2

A2 =	CК·VД·ρК·( FВ3·CВ + 0,8·α·S)+ (FП·CК + α·S)·CВ·VВ·ρВ	,
	(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) – 0,8·α^2·S^2

K =	α·S·( tВ31·CВ – tВ32·CВ)	,
	(FП·CК + α·S)·(FВ3·CВ + 0,8·α·S) -0,8·α^2·S^2

Маємо рівняння:

A1·p²·t_К(p) + A2·p·t_К(p) + t_К(p) = K·F_В3(p);

Передатна функція каналу F_В3 → t_К:

W_FВ3→tК(p) = t_К(p)/ F_В3(p) = K /(A1·p²+A2·p+1). (2)

Перехідна характеристика для каналу F_В3→t_К, при робочому режимі навантаження холодильника дистиляту, зображена на рисунку 1.3.

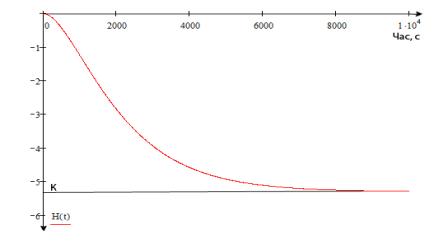
Рисунок 1.3 - Перехідна характеристика каналу F_В3→ t_К

Одержані в результаті моделювання рівняння (1, 2) складають статичну та динамічну моделі холодильника дистилята. Як видно з (рис. 1.3) та (2) об’єкт у динамічному відношенні представляє собою аперіодичну ланку другого порядку. Отримані моделі можна використати для розрахунку налаштування системи автоматичного регулювання даним апаратом. Враховуючі усі прийняті припущення областю застосування даної моделі є навчальний процес та попередні розрахунки при проектуванні систем регулювання.

Література:

1. Остапенко Ю.О. Ідентифікація та моделювання технологічних об’єктів керування / Ю.О. Остапенко – К: Задруга, 1999. – 420с.

2. Моделирование систем: метод. указания / сост.: С.В. Фролов, А.А. Третьяков, С.Б. Путин, С.А. Скворцов. – Тамбов : Изд-во Тамб. гос. техн. ун-та, 2007. – 32 с.