К.т.н. Гнусов Ю.В., Кубрак В.П.

Харьковский национальный университет внутренних дел

Экстраполяция тенденций

как способ прогнозирования преступности

Преступность как социально-экономическое явление формируется при воздействии многих факторов, однако выделить влияние каждого из них не представляется возможным, поэтому процесс прогнозирования показателей преступности рассматривается как функция времени. При таких условиях задачу прогнозирования следует понимать как экстраполяцию сложившихся во времени тенденций.

Общая задача экстраполяции заключается в нахождении значений некоторой функции, описывающей изменение показателя во времени, в точке, лежащей вне интервала наблюдения данной функции, что определяет возможность использования экстраполяции для целей прогнозирования. К настоящему времени экстраполяция нашла широкое применение как способ прогнозирования в силу простоты используемых прогнозирующих моделей и их физической интерпретируемости.

Экстраполяция определяет тенденции будущего развития исследуемого явления при условии, что закономерности данного явления, сложившиеся в прошлом, будут существовать и в будущем. Эти закономерности определяют наиболее устойчивые черты прогнозируемого процесса - его тренд, причем предполагается, что тренд может быть описан с помощью какой-либо функции.

Рассматриваемая экстраполяция основывается на следующих допущениях:

· развитие преступности как социально-экономического процесса может быть с достаточным основанием охарактеризовано плавной траекторией - трендом;

· общие условия, определяющие тенденции развития преступности в прошлом, не претерпят существенных изменений в будущем.

При данном подходе задача экстраполяции должна решаться в три этапа:

1) подбор вида функции тренда (структурная идентификация прогнозирующей модели);

2) определение параметров функции тренда (параметрическая идентификация прогнозирующей модели);

3) прогнозирование с помощью построенной модели.

Заметим, что как бы хорошо не была построена прогнозирующая модель (предиктор), прогноз непременно содержит ошибку, причем эта ошибка увеличивается с увеличением времени упреждения. Поэтому прогнозирование преступности с помощью экстраполяции наиболее целесообразно на короткие сроки. Естественно, что по мере поступления новой информации об изменении значений соответствующих показателей параметры функции тренда должны непрерывно усложняться. А это приводит к необходимости использования адаптивных методов.

Характерной особенностью временных рядов показателей преступности является наличие в них трендов или основных тенденций, сложившихся под влиянием наиболее типичных воздействий. Такой временной ряд можно описать некоторой дискретной функцией времени, которую целесообразно представить в виде суммы некоторой детерминированной функции и случайной составляющей:

n = 1, 2, 3, ... , (1)

где детерминированная функция является трендом, а случайная функция отражает воздействие на формирование преступности множества неучтенных факторов.

С теоретической точки зрения тренд преступности является результатом воздействия на ее формирование основных закономерностей причинно-следственного характера, регулирующих данный аспект динамики изменения прогнозируемых показателей. Воздействие же прочих факторов самой разнообразной природы носит в основном стохастический характер и отражается случайной функцией . Представление в виде суммы тренда и случайной составляющей удобно также тем, что при этом выделяется “управляемая” часть преступности, закономерности развития, которой с достаточной точностью могут быть определены, и “неуправляемая” стохастическая часть. Для описания тренда могут применяться самые различные функции, например, линейная, параболическая, степенная, экспоненциальная, модернизированная экспоненциальная, логистическая, 63%-ная функция, функции Гомпертца, Джонсона, Торнквиста, гиперболическая, экологическая и ряд других. На практике же наиболее часто применяют полиномиальные

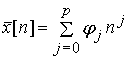(2)

или экспоненциальные

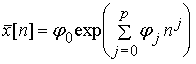(3)

функции.

Параметрам этих функций несложно придать качественный статистический смысл. Линейная функция x[n] = j₀ + j₁n, описывающая изменение преступности, определяется постоянным приростом j ₁ с начальным уровнем j ₀ . Парабола x[n] = j ₀ + + j ₁ n + j ₂ n² определяется постоянным темпом изменения абсолютного прироста 2 j ₂. Экспоненциальная функция ехр(j ₀ + + j ₁ n ) характеризует постоянный относительный рост q ^j1, а ехр (j ₀ + j ₁ n + j ₂ n² ) - постоянный относительный прирост q ^j2. Вообще же статистическая интерпретация трендов преступности многообразна, однако основное ее применение в анализе состояния и динамики изменения преступности заключается в определении основных направлений развития преступности как объекта исследования, выделении ее типичных черт и прогнозировании при выполнении задач планирования и управления деятельностью органов внутренних дел. Необходимо отметить, что проблема выбора конкретной кривой для описания тренда преступности является далеко не тривиальной, так как правильный или неправильный выбор может существенно повлиять на качество экстраполяции. Наиболее обоснованным представляется путь, когда форма кривой определяется в результате статистического анализа соответствующих показателей, который в большинстве случаев не удается провести ввиду ограниченности времени и средств. Кроме того, имеющиеся в информационных подразделениях МВД временные ряды, как правило, настолько коротки, что построенный на их базе тренд при дальнейшем росте объема выборки может не соответствовать реальному процессу или описываться совершенно другим типом кривой. Наиболее приемлемым является метод, который основывается на сравнении характеристик изменения приростов исследуемого временного ряда с соответствующими характеристиками кривых роста. Для описания тренда выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения фактических данных. Для устранения опасности выбора неадекватной кривой необходимо при выделении тренда либо аппроксимировать одиночные данные различными кривыми и проследить, как они будут вести себя в дальнейшем, либо осуществлять аппроксимацию с помощью системы ортогональных полиномов, например Лягерра, Эрмита, Чебышева и др. Начиная процесс экстраполяции с помощью функции невысоких степеней, мы всегда сможем по мере надобности ввести дополнительные члены, если выбранная исходная система по какой-либо причине не сможет нас удовлетворить. При этом необходимо всегда помнить, что применять следует полиномы невысоких степеней, так как в противном случае аппроксимирующие функции будут отражать случайные отклонения, а не тренд.

Рассмотрим некоторые процедуры оценивания параметров конкретных кривых, при этом будем полагать, что эти параметры входят в тренд линейно (либо путем некоторых преобразований исходная кривая может быть сведена к линейной по параметрам функции). Процедуры нелинейного оценивания значительно сложнее и менее разработаны. Итак, будем рассматривать процедуры определения коэффициентов тренда преступности типа (2). Заметим, что по теореме Вейерштрасса, прочие виды кривых мы можем с наперед заданной точностью аппроксимировать формами (2) и (3). Процедура оценивания коэффициентов, как это уже отмечалось во второй главе, является некоторым алгоритмом минимизации выбранного критерия идентификации Q . В теории и практике статистического оценивания используется целый ряд критериев, однако же в силу изложенных выше соображений, в первую очередь будут интересовать те, которые не связаны с какими-либо предположениями о статистических свойствах преступности. Это так называемые непараметрические критерии, основанные на рассогласовании между фактическими данными выбранного показателя и выходом предиктора (трендом). В общем виде эти критерии могут быть записаны в форме

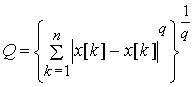(4)

При q=1 критерий (4) принимает форму критерия наименьших модулей, при q=2 - критерия наименьших квадратов, при - минимаксного критерия.

В практике прогнозирования используются, как правило, критерии наименьших модулей и наименьших квадратов, либо сводящиеся к ним, например, критерии вида:

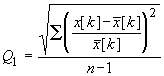; (5)

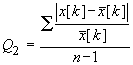. (6)

Наиболее распространенной схемой оценивания является аппроксимация по методу наименьших квадратов. Эта процедура обеспечивает минимизацию суммы квадратов независимо от статистических предположений. Критерий минимума суммы квадратов отклонений фактических данных от тренда обладает рядом достоинств, главными из которых являются следующие:

· критерий имеет достаточно ясный физический смысл - дисперсия выходного сигнала предиктора относительно процесса;

· критерий не использует никаких других предположений о случайных возмущениях, кроме предположения о существовании конечных дисперсий;

· при наличии гауссовских помех оценка по этому критерию дает наилучшее приближение;

· критерий достаточно удобен при проведении различных математических операций.

Эти обстоятельства обеспечили широкое применение данного метода в задачах прогнозирования.

Итак, пусть предиктор преступности описывается полиномом

; (7)

в качестве критерия идентификации используем квадратичную форму

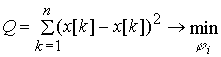. (8)

Дифференцируя (8) по j _i и приравнивая частные производные к нулю, получаем систему нормальных уравнений

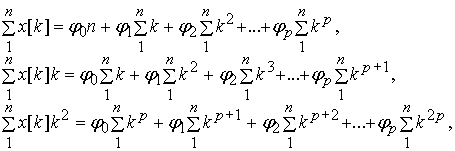(9)

где k - текущее дискретное время, пробегающее значения от 1 до n.

Решение данной системы в матричной форме имеет вид

, (10)

где 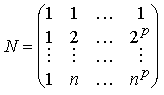, (11)

F=(j ₀, j ₁, ..., j _p)^T - вектор-столбец размерности (p+1) искомых коэффициентов модели, X[n] = (х[1], х[2], ..., х[n])^T - вектор-столбец размерности (n+1) имеющихся значений показателей, Т - символ транспонирования.

Прогноз с помощью предиктора (7) осуществляется подстановкой в уравнение в качестве аргумента будущего момента времени n+1.

Следует отметить, что даже при относительно небольших значениях n и p решение уравнения (10) на ЭВМ требует достаточно много времени и значительного объема оперативной памяти, что связано с необходимостью обращения матрицы . Таким образом, данная процедура плохо приспособлена для работы в реальном масштабе времени при прогнозировании преступности. Из других недостатков данной процедуры следует отметить то, что она учитывает все невязки с одинаковыми весами независимо от времени регистрации этих невязок. Таким образом, при построении предикторов преступности “устаревшие" данные могут оказать отрицательное влияние на точность прогноза.

Для целей оперативного прогнозирования преступности целесообразно использовать алгоритм текущего среднего, который осуществляет нахождение неизвестных коэффициентов на текущем интервале времени с применением метода наименьших квадратов. Этот алгоритм уже относится к адаптивным процедурам, поскольку в нем осуществляется отсеивание устаревшей информации. Используемый критерий идентификации имеет вид

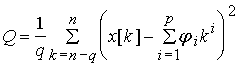, (12)

где параметр q определяет интервал усреднения.

Система нормальных уравнений в этом случае имеет вид

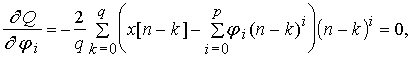(13)

где i = 0, 1,..., p.

Для упрощения выкладок введем обозначения

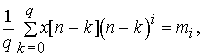i = 0, 1, 2, ... , p; (14)

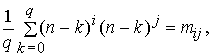i , j = 0, 1, 2, ... , p. (15)

Тогда система нормальных уравнений приобретает вид

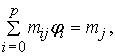j = 0, 1, 2, ... , p . или MF = m, (16)

где

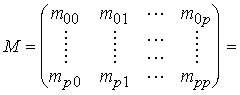
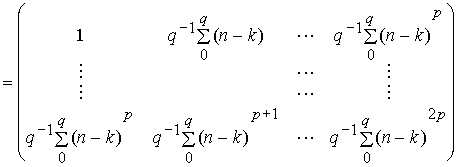, (17)

Отсюда i-ый коэффициент предиктора имеет вид

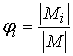, i = 0, 1, 2, ... , p , (18)

где матрица M_i отличается от M тем, что i-ый столбец в ней заменен столбцом m. Данная процедура значительно проще в реализации на ЭВМ, так как сводится в основном к вычислению определителей размерности (p+1)(p+1).