Зобачева А.Ю., Кашеварова Г.Г.

(Пермский государственный технический университет, г.Пермь, Россия)

Уточнение методики расчета узловых соединений элементов деревянных конструкций

В настоящее время наиболее распространенными сооружениями с применением клееных деревянных несущих и ограждающих конструкций являются склады калийных солей. Клеёные деревянные конструкции (КДК) не подвергаются разрушительному действию агрессивных сред минеральных удобрений, и поэтому срок службы сооружений с такими конструкциями определяется пределом морального старения объекта. Срок эксплуатации деревянных конструкций (в том числе и клееных) в условиях солевой агрессии превышает 40-50 лет без дополнительных затрат на защиту от коррозии.

Большой опыт применения деревянных клееных арок накоплен в Пермском крае при возведении складов минеральных удобрений на калийных предприятиях. Построено более 30 складов пролетами 18…60 м и более (за рубежом имеются примеры применения клееных арок пролетом до 250 м ), в которых в качестве несущих конструкций использованы стрельчатые арки и распорные конструкции треугольного очертания (А-образные арки).

Несмотря на широкое применение КДК в современном строительстве, напряженно-деформированное состояние большепролетных арок до сих пор изучено недостаточно полно, что сдерживает совершенствование нормативной базы разработку практических рекомендаций и по проектированию и расчету арочных конструкций.

Соединения являются наиболее ответственными частями деревянных конструкций. Для создания большинства строительных конструкций, отдельные части и элементы конструкции должны быть прочно и надежно соединены между собой.

От правильного конструктивного решения, расчета и изготовления соединений зависят деформативность, прочность, надежность и долговечность конструкций в целом. Анизотропия строения, малая прочность древесины при скалывании и растяжении поперек волокон и другие факторы значительно усложняют проектирование и расчет соединений деревянных конструкций.

При проектировании большепролетных арок и рам одной из проблем является устройство узловых соединений. Как правило, для устройства опорных и коньковых узлов арок и рам, применяют шарнирные узловые соединения в виде стальных башмаков, прикрепляемых к полуаркам с помощью стальных цилиндрических нагелей (болтов, шпилек, глухарей). Напряженное состояние такого узлового соединения достаточно сложное и характеризуется смятием древесины в зоне контакта торца элемента с опорной плитой башмака, скалыванием и раскалыванием древесины в зоне контакта древесины с нагелем и изгибом самого нагеля, работающего как балка на упруго-пластическом основании.

Существующая методика расчета соединений такого типа, рекомендуемая СНиП II-25-80, сводится к сравнению минимальной несущей способности нагеля из условия смятия древесины нагельного гнезда или изгиба самого нагеля с усилием, действующим на наиболее нагруженный нагель. Однако методики определения этих усилий в нормативной литературе не приводится.

В связи с вышесказанным вопросы рационального проектирования узловых соединений большепролетных деревянных клееных конструкций на стальных цилиндрических нагелях является весьма актуальной. Одним из путей решения данной проблемы может быть использование методов математического моделирования с использованием современных конечно-элементных программных комплексов и ЭВМ.

Для определения усилий в нагелях в зависимости от их количества, расположения и направления действия нагрузки использован ПК ANSYS. Решалась плоская задача, конструкция моделировалась двухмерными четырехугольными элементами PLANE82. Для упрощения рассмотрена только металлическая пластина, нагели моделировались с помощью закреплений. Для выявления зависимости реакций в нагелях проведен ряд вычислительных экспериментов. При этом использовалась математическая теория планирования эксперимента, где в качестве варьируемых факторов принимались: количество нагелей, расстояние по вертикали и горизонтали между ними, угол приложения силы, действующей на узел.

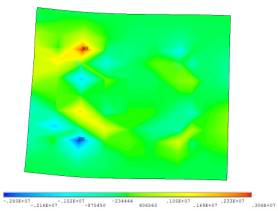
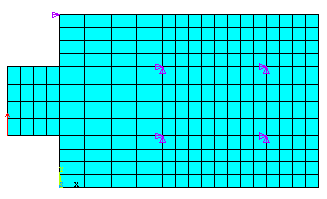
Рис.1 Конечно-элементная модель пластины и напряжения в пластине.

В существующей методике расчета (СНиП II-25-80) полностью игнорируются наличие силы трения по плоскости контакта древесина-металл, которая также будет препятствовать сдвигу. Поэтому на следующем этапе узел (рис.2) был смоделирован объемными конечными элементами SOLID95 с учетом контакта в плоскости соприкосновения торца деревянной части с опорной металлической пластиной и в зонах соединения древесины с нагелями. Использованы специальные контактные элементы: TARGE170 и CONTA173. При этом учтены ортотропные свойства древесины.

Полученные в результате расчетов зависимости дают возможность рационального подбора параметров соединения при проектировании большепролетных арок и рам.

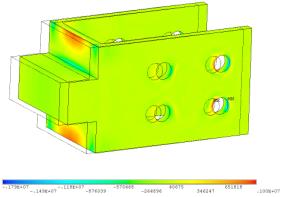
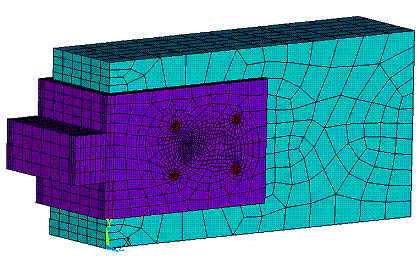
Рис.2 Конечно-элементная модель соединения и напряжения в пластине

Список литературы

1. СНиП II-25-80. Деревянные конструкции. Нормы проектирования.

2. Басов К.А. ANSYS: Справочник пользователя. – М.:ДМК Пресс, 2005. – 640с.