Савина С.В.

Финансовый университет при Правительстве Российской Федерации, Россия

Поведение интегралов одного класса на множестве бесконечно удаленных точек пространства

Рассмотрим поведение интегралов

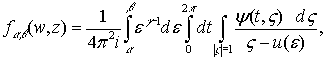(1)

где , где 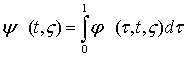, ─ действительные числа, на множестве бесконечно удаленных точек пространства .

Двумерное многообразие бесконечно удаленных точек пространства , которое обозначим через , состоит из точек вида , точек вида и точек [1].

Поведение интегралов (1) на множестве бесконечно удаленных точек пространства характеризует следующая теорема:

Теорема 1. Пусть функция такова, что интеграл

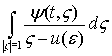
имеет равностепенно абсолютно непрерывные двойные интегралы по , где

.

Тогда интегралы (1) на двумерном многообразии бесконечно удаленных точек пространства обращаются в нуль, если точка (w,z) стремится к точкам вида и по любому пути, а к точке – по пути, принадлежащему гиперповерхности:

,

где b – любое действительное число.

► Пусть . Рассмотрим следующие области:

,,,

,

,

,

,.

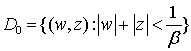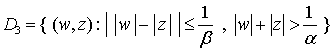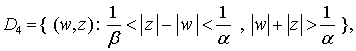
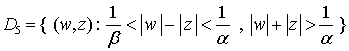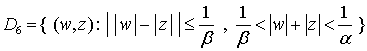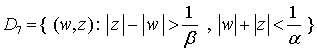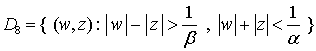Области являются областями аналитичности интегралов (1), а области – областями неаналитичности. Пусть точка по любому пути, принадлежащему области . Из задания следует, что

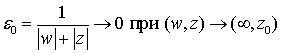, т.е. при .

Аналогично получаем, что

, ,

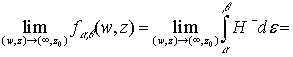
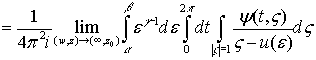.(2)

Так как , то при для всех

.

Используя теорему Витали [2], переходя к пределу в соотношении (2), получим:.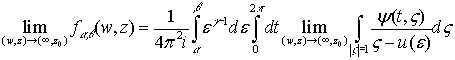

Внутренние интегралы есть интегралы типа Коши, поэтому, используя свойство интеграла типа Коши, а именно тот факт, что 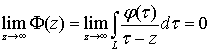(где L – произвольный замкнутый гладкий контур), получаем.

Пусть точка по любому пути, принадлежащему области . Проведя аналогичные рассуждения, получим, что

в области . Пусть теперь "отмеченным" способом, т. е. по пути, принадлежащему неаналитической гиперповерхности .

Вычислим : , (3)

где , причем .

Для точек равенство (3) запишется в виде:

.

Нетрудно установить, что коэффициент при положителен при всех значениях , кроме точек множества ,

плоская лебегова мера которого равна нулю.Тогда при стремлении точки "отмеченным" способом .

Проведя изложенные выше рассуждения, получим . ◄

Литература:

1. Хвостов А.Т. Поведение интегралов типа Темлякова в области неаналитичности. – Дисс. … канд. физ.-мат. наук. – М., 1967. – 82 с.

2. Натансон И.П. Теория функций вещественной переменной. – М.: Наука, 1974.