Математика/5. Математическое моделирование
Студент. Быкова О.А.
Новосибирский государственный технический университет, Россия
Разработка математической модели добычи газовых
гидратов
Наиболее распространенным газом,
формирующим газогидраты является метан. Исследования последних двух десятилетий
показали, что залежи гидрата метана в толще вечной мерзлоты на суше и под
океанским дном могут соперничать со всеми обычными месторождениями
энергоносителей. По предварительным оценкам, общие объемы метана в природных
гидратах оцениваются огромными цифрами - от 3000 до 7000 трлн. м3.
Для сравнения, оценка оставшихся и неоткрытых мировых запасов традиционного
природного газа составляет всего около 370 трлн. м3 [1]. Кроме
этого, горение метана выделяет значительно меньше СО2 в атмосферу,
чем сжигание угля или нефти.
В настоящее время для большинства ученых
развитых стран первоочередной задачей становиться изучение и последующая добыча
альтернативного топлива будущего – газовых гидратов [2].
Газовые гидраты (также клатраты) -
кристаллические соединения, образующиеся при определенных термобарических
условиях из воды и газа [3].
Ученые утверждают, что добыча газогидратов
может только усугубить глобальное потепление, поскольку метан является одним из
главных виновников так называемого «парникового» эффекта. Но с другой стороны
нельзя исключать возможность неконтролируемого выделения метана в результате
повышения температуры. Поэтому необходим наиболее безопасный и экологически
правильный способ освоения залежей гидратов, который, в случае успеха, подавит
всю критику.
Одним из таких методов освоения
газогидратов может оказаться схема добычи газогидратов [4] рисунок 1, состоящая
из:
·
тепловыделяющего
элемента, который изготавливают из отработанного ядерного топлива АЭС;
·
скважины и гибких
трубопроводов, предназначенных для транспортировки жидкой пульпы;
·
центрифуги для
разделения газа, жидкости и примесей из пульпы;
·
устройства по сжижению
газа за счет повышения давления
и
умеренном понижении температуры;
·
гибких трубопроводов,
выдерживающих давление;
·
плавающей затопленной
платформы для накопления сжиженного газа;
·
плавающего причала для
танкера;
·
подводной станции из
современных прочных материалов;
·
автоматической системы
управления;
·
микросейсмики для
разведки трещин и контроля за разгазированием газогидратного пласта.
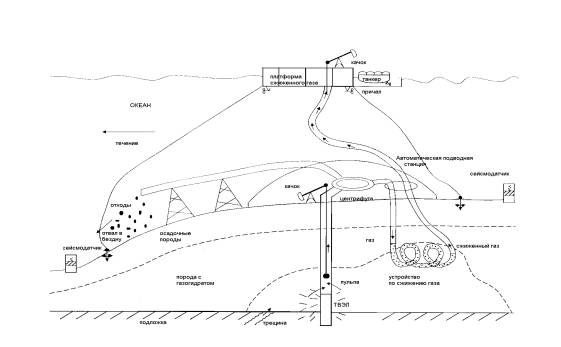
Рис. 1 – Схема добычи газовых
гидратов
Рассмотрим односкоростную n-компонентную смесь, аналогично тому, как это сделано
в работе [5]. Выпишем уравнения, выражающие законы сохранения, массы, импульса
и энергии для i-ого компонента смеси,
относящийся к фиксированному в пространстве конечному объему V, и которые имеют вид:
![]() , (1)
, (1)
![]() , (2)
, (2)
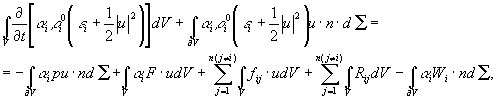 (3)
(3)
где u – вектор скорости; n – внешняя
единичная нормаль к поверхности ![]() , ограничивающей рассматриваемый объем V;
, ограничивающей рассматриваемый объем V; ![]() - объемная доля i-й
фракции в смеси;
- объемная доля i-й
фракции в смеси; ![]() - интенсивность
превращения массы из i-й фракции в j-ю в единице объема смеси; F – плотность массовой силы;
- интенсивность
превращения массы из i-й фракции в j-ю в единице объема смеси; F – плотность массовой силы; ![]() - силы
межфракционного взаимодействия между i-й и j-й составляющими, приходящаяся на единицу объема
смеси;
- силы
межфракционного взаимодействия между i-й и j-й составляющими, приходящаяся на единицу объема
смеси; ![]() - удельная внутренняя
энергия i-го компонента;
- удельная внутренняя
энергия i-го компонента; ![]() - тепловыделение в
единицу времени на единицу объема смеси, возникшее вследствие превращения i-й фракции в j-ю;
- тепловыделение в
единицу времени на единицу объема смеси, возникшее вследствие превращения i-й фракции в j-ю; ![]() - количество тепла в
единицу времени на единицу объема смеси, которое поступает i-й фракции от j-ю вследствие излучения;
- количество тепла в
единицу времени на единицу объема смеси, которое поступает i-й фракции от j-ю вследствие излучения; ![]() - вектор плотности
теплового потока, связанный с температурой
- вектор плотности
теплового потока, связанный с температурой ![]() законом Фурье:
законом Фурье:
![]() (4)
(4)
где ![]() - коэффициент
теплопроводности, относящийся к i-й фракции.
Передача тепла по закону Фурье происходит лишь в тех компонентах, которые в
связанном виде заполняют занятое средой пространство. Например, в пузырьковой
жидкости фракцией проводящей тепло является жидкий компонент.
- коэффициент
теплопроводности, относящийся к i-й фракции.
Передача тепла по закону Фурье происходит лишь в тех компонентах, которые в
связанном виде заполняют занятое средой пространство. Например, в пузырьковой
жидкости фракцией проводящей тепло является жидкий компонент.
Рассматриваем приближенную модель, в
которой ничтожно малы значения ![]() , расчет ведется до центрифуги, также
, расчет ведется до центрифуги, также ![]() =0 и
=0 и ![]() =0, так как нет фазового перехода. Поэтому данные параметры
не учитываются при построении математической модели до центрифуги. В устройстве
же по сжижению газа значение
=0, так как нет фазового перехода. Поэтому данные параметры
не учитываются при построении математической модели до центрифуги. В устройстве
же по сжижению газа значение ![]() значительно
относиться к фазовому переходу.
значительно
относиться к фазовому переходу.
В силу произвольности выбранного жидкого
объема, из интегральных законов сохранения следует их дифференциальная форма.
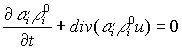 , (5)
, (5)
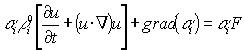 , (6)
, (6)
![]() (7)
(7)
Если просуммировать каждое из уравнений
(5)…(7) по индексу i от 1 до n, то
получим законы сохранения массы, импульса и энергии для смеси в целом:
![]() , (8)
, (8)
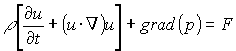 , (9)
, (9)
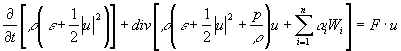 , (10)
, (10)
где ![]() - удельная внутренняя
энергия смеси, определяемая из выражения:
- удельная внутренняя
энергия смеси, определяемая из выражения:
![]() (11)
(11)
Уравнения (8)…(10) выражают классические
законы сохранения массы, импульса и энергии, таким образом, многофазная модель
в виде уравнений (5)…(7) находится в полном соответствии с физической моделью
механики сплошной среды.
В дальнейшем предполагается осуществить
расчет движения среды на различных этапах в соответствии со схемой на рисунке
1. Для описания движения пульпы в скважине и трубопроводе до центрифуги предполагается
рассмотреть трехфазную математическая модель, а в устройстве по сжижению газа –
двухфазную модель, в которой будет учитываться фазовый переход.
Литература
1.
Т. С. Коллет, Р. Льюис,
У. Такаши. Растущий интерес к газовым гидратам // Schlumberger. Нефтегазовое
обозрение. - 2001. - Т.6. - №2. - С. 38–54.
2.
В. А. Соловьёв.
Природные газовые гидраты как потенциальное полезное ископаемое // Российский
химический журнал. - 2003. - Т. 48. - №3. -
С. 59-69.
3.
Ю.А. Дядин, А.Л. Гущин.
Газовые гидраты // Соросовский образовательный журнал. - 1998. - №3. - С. 55–64.
4.
В.В.Хабиров,
С.В.Хабиров. Разработка газогидратов современными технологиями // Труды
Института механики УНЦ РАН. Уфа. - 2010. - С. 210-230.
5.
В.С. Суров.
Односкоростная модель гетерогенной среды с гиперболичным адиабатическим ядром //
Журнал вычислительной математики и математической физики. - 2008. – Т.48. - №6.
- С. 1-15.