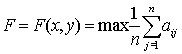Педагогические науки/1. Дистанционное образование
О.А. Гнездилова, Д.э.н.,
профессор Н.В. Мордовченков
филиала Сочинского
государственного университета туризма и курортного дела в г. Нижний Новгород
Инновационная инфраструктура
дистанционного обучения в процессе управления знаниями
В условиях постиндустриальной экономики
продолжается поиск методолого-теоретической парадигмы инновационной
модернизации образования. На каждом этапе функционирования социума существует
система институтов, выполняющих важнейшие жизненные потребности общества. При
этом деятельность социальных институтов регламентирована устоявшимися
традициями, правовыми нормами, менталитетом в пределах правовой инфраструктуры.
По
нашему мнению необходимо сформировать экономически обоснованную институциональную
инфраструктуру дистанционного обучения (рис. 1).


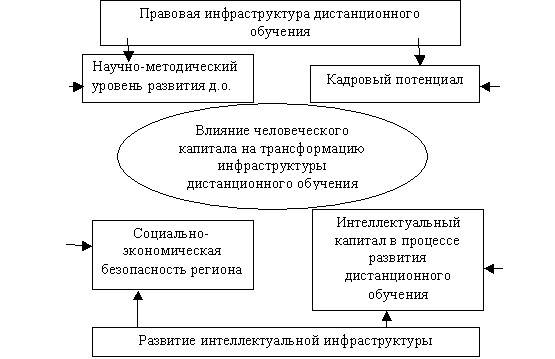

Рис. 1 Влияние человеческого капитала на трансформацию
инфраструктуры дистанционного обучения
Разработанная авторами статьи методика
оптимизации процесса дистанционного обучения по созданию эконометрических
моделей может быть использована министерством образования и науки региона для
повышения эффективности научно-образовательной инфраструктуры на мезоуровне с
использованием компьютерных информационных технологий.[1],[2]
Авторы статьи солидарны с тем, что без
широкого применения эконометрики в доступной для студента форме от вузовской
науки невозможно ожидать полезных результатов, а поэтому необходимо новое
направление в инновационной инфраструктуре высшей школы (дистанционное
обучение) – инфраэконометрика, позволяющая решать инфраструктурные проблемы в
образовании посредством эффективных управленческих решений в комплексной
системе эконометрических методов и моделей.
Опыт и перспектива использования
эконометрических методов и моделей свидетельствует, что степень эффективности
выбора конкретного управленческого решения может быть оценено в виде отклика F,
имеющего количественную интерпретацию (таблица 1).[3]
Вместе с тем система факторов, влияющих
на функцию полезности, в условиях создания институциональной инфраструктуры
следует классифицировать:
1) факторы Х1, Х2, …, XL,
выбор которых определяется акторами, принимающими управленческие решения.
2) факторы, характеризующие
условия рисков и неопределенности, в которых осуществляется выбор и на которые
акторы, принимающие решения, влиять не могут. В перечень неконтролируемых
факторов может быть и лаг по времени t. Неконтролируемые
факторы в зависимости от информированности о них подразделяют на три подсистемы:
а) неконтролируемые факторы А1, А2, …, АР – неслучайные
фиксированные величины.
б) вероятностные неконтролируемые факторы Y1, Y2,
…, Yg – случайные величины и процессы с известными законами
распределений.
в) неконтролируемые факторы Z1, Z2,
…, ZZ, для каждого из которых известна только генеральная
совокупность, внутри которой находится закон распределения, значения
неопределённых факторов неизвестны в момент принятия решения.
В
соответствии с хрестоматийной классификацией факторов критерий оптимальности
следует представить в виде:
F = F (X1, X2, …,
XL, A1, A2, …, AP, Y1, Y2, …, Yg, Z1, Z2, …, ZZ, t)
Значения контролируемых факторов, как правило,
имеют область допустимых значений, например, ограниченностью имеющихся
ресурсов. Так при фиксируемых подсистемах Ωх1, Ωх2, …, ΩхL, в
которых оказывают воздействие реально существующие факторы X1, X2,
…, XL. Аналогично неконтролируемые факторы могут иметь дискретный
характер. Параметры A, Y, Z
могут иметь идентификационные типы в скалярном или матричном виде, а также
интерпретироваться из векторной алгебры или представлять тригонометрическую
функцию.
В
связи с тем, что критерий оптимальности – это количественная мера степени
достижения цели управления, математически цель управления выражается в
стремлении к максимально возможному увеличению (или уменьшению) значения
критерия F, что можно записать в виде: F max
(или min).
Средством
достижения этой цели является соответствующий выбор управлений X1, X2,
…, XL из подсистем Ωх1, Ωх2, …, ΩхL их
допустимых значений. В целом задача качественного управления знаниями может
быть сформулирована следующим образом: при заданных значениях и характеристиках
фиксированных неконтролируемых факторов A1, A2,
…, AP, Y1, Y2,
…, Yg с учетом неопределенных факторов Z1, Z2,
…, ZZ найти оптимальные значения X1опт, X2опт,
…, XLопт из подсистем возможного управления процессом дистанционного
обучения Ωх1, Ωх2, …, ΩхL фиксированных значений,
имеющие разброс в максимум (минимум) по критерию оптимальности F.[3]
Мы солидарны с таким подходом, который может быть применим и развиваться в
системе формирования и функционирования экономически и социально обоснованного
дистанционного обучения, при котором в качестве приоритета может быть
представлена функция полезности встроенная не только при формировании и
трансформации института: общество-экспресс-образование, но и при создании
интеллектуальной инфраструктуры (человеческого капитала).
Авторы
статьи солидарны с мнением ученных, что инновационная инфраструктура в
значительной мере коррелирует с конкурентоспособной доктриной высшего
образования и науки при формировании конкурентно способного инноватора XXI
века.