Педагогические науки / 5. Современные методы преподавания

Тулученко Г.Я.

Херсонский национальный технический университет, Украина

Организация самоконтроля знаний студентов с помощью СКМ Maple при изучении методов интегрирования

тригонометрических выражений

Возможность проведения операции аналитического интегрирования и интуитивно понятный синтаксис соответствующей команды делают систему компьютерной математики (СКМ) Maple удобным для студентов инструментом самоконтроля правильности выполнения заданий, в частности, во время самоподготовки.

Значительное сокращение часов на изучение высшей математики в технических вузах, происходящее последнее время в Украине, приводит к тому, что излагаются только основные методы интегрирования произведений тригонометрических функций в натуральных степенях, ориентированные на "ручное" применение [1-5]. Поэтому для большинства студентов инженерных и экономических специальностей является неожиданностью, когда СКМ Maple для отдельных видов названых произведений формирует ответ в виде, отличном от ожидаемого при обучении стандартным приемам интегрирования [3, 5].

Под стандартными приемами понимается вычисление интегралов вида , по разным алгоритмам в результате предварительной классификации по наличию или отсутствию хотя бы одного нечетного показателя степени. Менее распространенным является общий подход к обоим случаям, который состоит в использовании рекуррентных формул. Существование различных приемов интегрирования этих выражений и приводит к появлению разных по внешнему виду, но тождественных между собой, ответов.

Пример 1. Вычислить интеграл .

1) Традиционно определяем наличие нечетной степени – третьей, и выполняем интегрирование по стандартному алгоритму:

.

(1)

2) СКМ Maple в этом случае предлагает такой ответ:

f:=sin(x)^3: int(f,x);

(2)

Полученный вид ответа соответствует использованию рекуррентной формулы [2, 4]:

, .

(3)

Возникающая проблемная ситуация позволяет активизировать учебную деятельность студентов за счет дополнительных заданий:

1) Проверить, является ли предложенная СКМ Maple в качестве ответа функция – первообразной для функции ? Что другими словами означает проверку: могла ли СКМ Maple ошибиться?

2) Доказать тождественность выражений (1) и (2).

3) Воспроизвести алгоритм решения примера СКМ Maple. Ведь нелогично получать ответ в виде (1) и использовать основное тригонометрическое тождество, чтобы перейти к виду (2).

4) Вывести рекуррентную формулу (3).

Выполнение заданий 1)-2) обычно не вызывает трудностей. Задания 3)-4) не являются тривиальными. Они рассчитаны на студентов с хорошей математической подготовкой и способствуют установлению внутрипредметных связей между разными методами интегрирования (в данном случае между методом интегрирования по частям и методами интегрирования тригонометрических выражений):

.

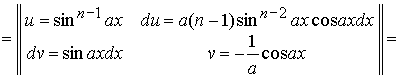
Обозначим заданный интеграл и найдем его значение из уравнения: ;

;

.

При выполнении задания 3) студентами чаще всего предлагается использование формулы тройного угла:

.

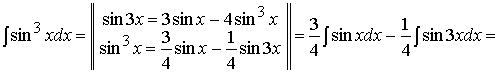
Что приводит к еще одному виду ответа и усиливает интригу: так как же "думает" компьютер?

Таким образом, вычисление в СКМ Maple интегралов от степеней тригонометрических функций: синус и косинус, – и их произведений, происходит по рекуррентным формулам, аналогичным формуле (3) [2, 4]. В случае интегрирования выражений, содержащих хотя бы одну из названых функций в нечетной степени, т.е. при вычислении интегралов вида:

1) , ;	3) , ;
2) , ;	4) , .
5) , ,

структура ответа будет существенно отличаться от ответа, полученного с применением методов, основанных на учете четности/нечетности показателей степеней.

Рассмотренный пример показывает, как применение информационных технологий при преподавании такой классической дисциплины как высшая математика способствует активизации учебной деятельности, повышению интереса к изучению методов интегрирования. СКМ Maple позволяет на новом уровне раскрывать перед студентами взаимные связи между разными методами интегрирования, демонстрировать примеры целесообразности применения разных методов интегрирования при вычислении одного и того же интеграла в "ручном" и компьютерном исполнении.

Литература

1. Демидович Б.П. Сборник задач и упражнений по математическому анализу / Б.П. Демидович. – М.: Наука, Гл. ред. физ.-мат. лит., 1977. – С. 170–171.

2. Минорский В.П. Сборник задач по высшей математике / В.П. Минорский. – М.: ФИЗМАТЛИТ, 2001. – С. 148–150.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т.1 / Н.С. Пискунов. – М.: Наука, Главная редакция физико-математической литературы, 1985. – С. 343–345 .

4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2 / Г.М. Фихтенгольц. – М.: ФИЗМАТЛИТ, 2001. – С. 76–80.

5. Фролов С.В. Курс высшей математики / С.В. Фролов, Р.Я. Шостак . – М.: Высшая школа, 1966. – С. 321–323.