Павлов А. М.

Восточно – Казахстанский университет им. Аманжолова.

Усть – Каменогорск. Казахстан.

ОПРЕДЕЛЕНИЕ СРЕДНЕГО РАССТОЯНИЯ МЕЖДУ МОЛЕКУЛАМИ

В КЛАСТЕРЕ С ПОМОЩЬЮ ТЕОРЕМЫ ВИРИАЛА.

До сих пор теорема вириала использовалась для получения уравнения состояния газов. Однако с помощью этой теоремы можно определить среднее расстояние между молекулами в димере и в более крупном кластере, а также плотность конденсированного состояния вещества.

Как известно, теорема вириала гласит:

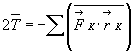(1)

и для потенциальных сил

, (2)

где -средняя кинетическая энергия,U-потенциальная энергия.

Правая часть равенств (1) и (2) называют вириалом, а сами эти равенства выражают теорему вириала.

Рассмотрим несколько примеров использования этой теоремы:

а) Ньютоновское взаимодействие. В этом случае

и значит

Следовательно,

Полная энергия системы равна

При будет и . Это условие финитного движения. Из связи и можно найти первую космическую скорость:

и .

б) Взаимодействие, описываемое потенциалом Леннарда-Джонса (6 –12):

.

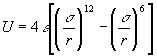Теперь

.

Значит

,

где 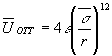и .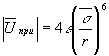

Полная потенциальная энергия равна

,

а полная энергия системы будет

. (3)

Для образования простейшего кластера – димера необходимо, чтобы было . Тогда оказывается, что

(4)

Подставив сюда значения и , получаем

,

где - диаметр молекулы. Напомним, что равновесное расстояние, при котором , равно .

При . Чтобы было необходимо, чтобы было меньше указанного значения. Средняя потенциальная энергия при равна . Эту величину можно было бы считать энергией связи системы, если бы кинетическая энергия равнялась нулю. Но кинетическая энергия равна и .

Напомним, что здесь речь идет о средней энергии относительного движения. Центр масс системы может иметь определенную скорость и в лабораторной системе отсчета .

Если среднее расстояние между молекулами известно, то зная , можно рассчитать плотность вещества, состоящего из данных частиц. В самом деле, если между частицами расстояние , то размер шара, занимаемого одной молекулой, будет и объем, приходящийся на один киломоль таких частиц, будет

.

Тогда плотность вещества равна

. (5)

Например, у молекулы азота . Тогда и, так как , . Плотность твердого азота составляет , а жидкого - . Погрешность определения плотности твердого азота составляет 8%. Примерно с такой же погрешностью определяется диаметр молекул .

Ещё один пример. Диаметр молекулы кислорода и , . Тогда из (5) следует, что плотность конденсированного кислорода должна быть . Однако плотность твердого кислорода составляет , а жидкого - . Снова плотность той и другой фазы меньше. Однако разброс в значениях достаточно большой: от до . Если взять последнее значение , то будет .

Таким образом, можно констатировать, что с помощью теоремы вириала можно определять средние расстояния между частицами в твердой фазе и плотность этой фазы. Однако, необходимо отметить: поскольку расчетное значение плотности твердого тела получается почти всегда больше табличной, то в твердом теле нет плотной упаковки частиц. Об этом же говорит наличие диффузии в твердых телах.

Поскольку разность между плотностью жидкой фазы и рассчитанной по (5) ещё больше, то в жидкости упаковка молекул ещё реже. Промежутки между молекулами и микрополости занимают достаточно большой объем. Так в азоте этот объём составляет порядка в , а в кислороде - в 1 куб. метре.

Литература.

1. Цянь Сюэ – Сень. Физическая механика. – М.: Мир. – 1965 стр 316.

2. Енохин А. С. Справочник по физике и технике. – М.: Просвещение, 1989, - 224 с.

3. Голдстейн Г. Классическая механика.-М.; Наука,-415 с.