Физика/2.Физика твердого тела.

Вазанков Д.Б., Осика Д.В., Топчий А.О.

Автомобільно-дорожній інститут донецького вищого навчального закладу Донецького Національного Технічного Університету, Україна

Дифузія точкових дефектів у полі градиенту напружень.

Різноманітні дослідження дифузії точкових дефектів в полі градієнта напружень дають різні результати. Відмінність між результатами обумовлена, насамперед, різними постановами задачі для термодинамічних систем, для яких отриманий хімічний потенціал. Градієнт хімічного потенціала раніше враховувався як сила, що призводила до руху точкових дефектів в визначеному напрямку. Виведене таким чином рівняння дифузії може використовуватися для різних спеціальних випадків і описує сумарний потік дефектів. Термодинамічні аргументи визначають граничні умови при русі дефектів до стоків чи від джерел. Граничні умови визначають кінцевий розподіл та концентрацію дефектів. Рівняння дифузії в полі градієнта напружень отримане для даної проблеми може використовуватися для дослідження дифузії в пластині. Вирішення даної проблеми з істинними граничними умовами отримане для сумарного потоку дефектів з однієї поверхні на їншу. Рівняння показує, що потоки дефектів ідентичні мікроскопічним потокам дефектів, коли концентрація дефектів в кристалі дуже близька до рівноважної.

Дифузійне рівняння

Для виведення рівняння дифузії в полі градієнта напружень Кохлер вирішив використовувати приріст енергії в атомі в сідловій точці конфігурації. Цей приріст енергії точно виражається через міжатомний потенціал, або приріст міжатомної відстані. Останній виражається через пружню деформацію. Після того, як Кохлер включив приріст енергії дефектів в дифузійне рівняння, стало можливим використовувати для ситуацій, при яких концентрація дефектів дуже близька до рівноважної. У випадку великого пересичення прикладене напруження лише змінює кінетику міграції дефектів та дію повехневих стоків.

При виведенні рівняння дифузії також застосовується активаційний об’єм для міграції:

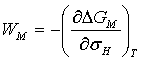(1)

де - феноменологічний параметр, - вільна енергія міграції, - гідростатичне напруження.

Дифузійне рівняння виводиться за допомогою врахування атомних потоків дефектів з одного стійкого положення рівноваги до сусіднього положення. Якщо потік одного напрямку ; потік з протилежного напрямку - , то сумарний потік дефектів будемо позначати – j. Потоки , визначені концентраційними та активаційними бар’єрами відносно початкового стійкого положення рівноваги: енергії кінцевого стійкого положення рівноваги не має значення для індивідуальних потоків та .

Якщо С(х) - розподіл концентрації через визначений час, то потоки дефектів між суміжними стійкими конфігураціями:

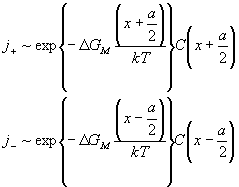
Тоді сумарний потік точкових дефектів:

Загальний потік дефектів описується виразом:

, (2)

де використане рівняння (1). Коефіцієнт дифузії для міграції під впливом локального гідростатичного напруження:

, (3)

де D(0) – коефіцієнт дифузії для міграції дефектів в ненапруженому кристалі.

Користуючись рівнянням неперервності та (2) - (3) рівняння дифузії може бути записано у вигляді:

(4)

Граничні умови

Розглянемо дифузію вакансій через площину товщиною (b-a) при постійній температурі, враховуючи дію напруження на вільну поверхню. Вважаємо, що поверхня є ідеальним стоком та джерелом дефектів.

Приріст вільної енергії дорівнює нулю, коли вакансії створюються поблизу поверхні. Тоді:

, (5)

де - енергія утворення вакансії у вільно напруженому кристалі, С₀ - рівноважна концентрація вакансій, - атомний об’єм, - енергія пружнього зв’язку, а:

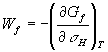(6)

- це частковий молярний об’єм, - вільна енергія утворення вакансій. З (5) та (3) випливають граничні умови поблизу поверхонь х = а та х = b :

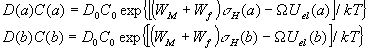(7)

Для стаціонарної ситуації: , а розв’язок рівняння дифузії (4) задовільняє граничним умовам:

(8)

Потік вакансій з поверхні в об’єм кристалу:

(9)

або

(10)

Концентрація вакансій всередині кристалу дає рівноважні умови (5), тому рівняння потоку (10) може бути узагальнене і отримає вигляд:

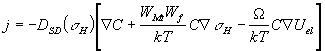(11)

З урахуванням енергії пружнього зв’язку:

, (12)

де К –об’ємний модуль, G – модуль зсуву а:

(13)

рівняння (11) прийме вигляд:

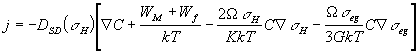, (14)

а коефіцієнт самодифузії буде визначатись такою формулою:

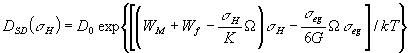(15)

З усього вище наведеного можна сказати що, в області дуже низьких напружень (порядку декількох одиниць кгс/мм²) і температур деформування (Т « Т_кр) гетерогенно-дифузійний процес деформації цілком переходить у чисто дифузійний, у тому розумінні, що як створення первинних зародків мікродеформації у виді дислокаційних петель, так і їхнє подальше зростання цілком відбувається за рахунок дифузійних процесів. При цьому, внаслідок загального зниження хімічного потенціалу вакансій при стисканні, а, також, за рахунок різниці хімічних потенціалів вакансій у неоднорідному полі напружень (на торцях, преципітатах) виникають спрямовані дифузійні потоки і виникають дифузійні процеси конденсації вакансій на стоках (наприклад, на вакансійних кластерах та ін.) з наступним захлопуванням вакансійних кластерів і утворенням дислокаційних петель.

ЛІТЕРАТУРА:

1. Swarezentruber B.S.// Phys. Rev. Lett. – 1996, v. 76, №3. - c. 459-462.

2. W.G. Wolfer. Diffusion of point defects in a stress gradient. //Scripta METALLURGICA, 1971, 5, №11, р. 1017 – 1022.

3. Абызов А.С., Слезов В.В., Танатаров Л.В. О роли вакансий в релаксации напряжений вокруг растущего включения новой фазы.// ФТТ, 1991, т. 33, №3. – с. 973 – 975.

4. Александров Я.Н., Зотов М.И. Внутреннее трение и дефекты в полупроводниках. – Новосибирск, 1979.

5. Алехин В.П. Физика прочности и пластичности поверхностных слоев материалов. М.:Наука, 1983.- 280 с. Блейкли Д.М. Поверхностная диффузия. М.: Металлургия, 1965. – 127 с.

6. Болотов В.В., Васильев А.В., Смирнов Л.С. Об знергии миграции простейших дефектов в германии и кремнии.// ФТП. – 1974, т. 8, вып.3. – с.518-521.

7. Болтакс Б.И. Диффузия и точечные дефекты в полупроводниках. М: Гос. изд-во физико-математической литературы, 1961. – 461 с.

8. Бургуэн Ж., Ланно М. Точечные дефекты в полупроводниках. Экспериментальные аспекты. М.: Мир, 1985. – 304 с.

9. В.А. Пантелеев, Н.Е. Рудой. // ФТП, 4, 1970, с. 1368.