SNR calculations for magnetic nanoparticles under asymmetric stochastic resonance conditions

A.G. Isavnin, I.I.Mirgazov

Kazan (Volga region) Federal University, Russia

Stochastic resonance phenomenon has been well investigated in various areas, including magnetic nanoparticles systems [1,2]. In some previous papers the effect was considered as application to superparamagnetic particles, with noise intensity measure being temperature of the sample and external periodic signal being weak radiofrequency field [3,4]. There are two commonly used approaches to describe the system behavior under such conditions: the two-state model, based upon the master equation for Kramers escape rates [5], and the continuous model, based upon numerical solution of the Fokker-Planck equation with a periodic drift term [6]. The influence of additional permanent magnetic field, applied at different angles to the “easy axis”, to dynamic magnetic susceptibility was also thoroughly explored before [7-9]. Here we present calculations for output signal-to-noise ratio (SNR) of the system of magnetic nanoparticles with auxiliary permanent magnetic field applied at arbitrary angle. Along with dynamic magnetic susceptibility, SNR is the most important characteristic of stochastic resonance. As usually we consider thermal switches of the particle magnetic moment as internal noise of the system, and output signal is assumed to be regular part of the magnetic moment motion at frequency of external weak radiosignal.

So, the energy of single-domain particle with uniaxial magnetic anisotropy is _, (1)

Here the first term describes interaction of the magnetic moment of superparamagnetic particle with anisotropy field (K is anisotropy constant, v is the particle’s volume, q is the angle between magnetization vector and easy axis); the second term is associated with permanent magnetic field Н applied at angle α to the axis of easiest magnetization; the last term represents interaction with radiofrequensy field.

We use the two-state model or the discrete-orientations approximation in our calculations. Therefore the magnetic moment of the particle is allowed to be in just two states corresponding two minima of the double well. It is convenient to define discrete variable x=Mcosq describing projection of the magnetization vector to the easy axis. So, this variable can take only two values. The two-state theory used trough this paper implies that instead of continuous diffusion of the particle’s magnetic moment over a sphere we consider its stochastic switches between two directions. Advantage of such approximation is possibility of using the master equation for transition rates that yields analytical solution. The master equation is [3]:

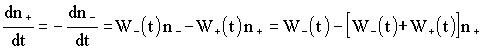. (2)

Here n_± is the probability of discrete variable x=Мcosq to take value x_±. W_±(t) is escape rate from ± state corresponding to stable directions of the magnetic moment. The analytical solution of (2) for asymmetric double-well potential was obtained in [8]:

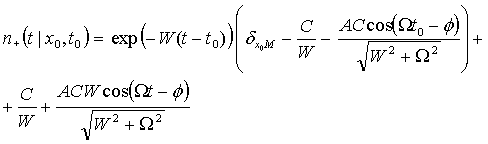_{, (3)}

where

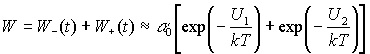_{, (4)}

and the escape rates of the magnetic moment over potential barriers:

_{, . (5)}

Here C=a₀exp(-U₁/(kT)) is the Kramers escape rate from the lower minimum of the stationary asymmetric potential. f=arctg(W/W) is the phase shift between response of the system and external periodic signal. It was shown in [9] that |cosq_min- | » |cosq_min+ | when m₀МH < K, so for simplicity we assume A₊=A_-=A. Here is a dimensionless amplitude of the external modulation’s projection to the “easy axis”. Let us denote also M₀=Mcosq_min- . The attempt frequency a₀ is usually of order of 10⁹ - 10¹⁰ s^-1 for fine ferromagnetic particles. More precise expression for the attempt frequency can be found in [10].

The autocorrelation function has the form [5]:

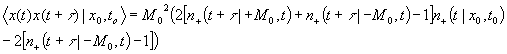_{. (6)}

So we have calculated it for our case in the limit of t₀ →∞ : (7)

_.

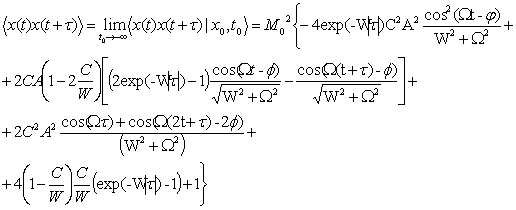The averaged over t autocorrelation function is

_{. (8)}

The power spectrum of the system as Fourier transform of the autocorrelation function is (9)

_.

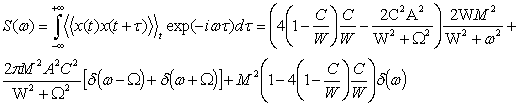We are interested in values that have physical meaning, so one can consider the result only for positive frequencies:

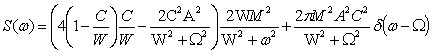_{. (10)}

_{Signal-to-noise ratio is defined as ratio of output power of the signal to output power of noise at frequency of external signal. So after integrating of the second term over ω and taking noise power at unity frequency interval near Ω we obtain}

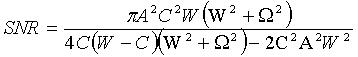_{. (11)}

The temperature dependence of the SNR continuously reveals well known nonmonotonous bell-shape form with distinct maximum.

REFERENCES

1. Fauve S., Heslot F. // Phys.Lett.A. (1983), V.97, P.5-7.

2. Jung P., Hanggi P. // Europhysics Letters (1989), V.8, N 6, P.505-510.

3. Sadykov E.K., Isavnin A.G. // Physics of the Solid State (1994), V.36, N 11, P.1843-1844.

4. Sadykov E.K., Isavnin A.G. // Hyperfine Interactions (1996), V.99, P.415-419.

5. McNamara B., Wiesenfeld K. // Phys.Rev.A (1989), V.39, N 9, P.4854-4869.

6. Gang H., Nicolis G., Nicolis C. // Phys.Rev.A (1990), V.42, N 4, P.2030-2041.

7. Isavnin A.G. // Russian Physics Journal (2005), V.48, N 5, P.511-515.

8. Isavnin A.G. // Russian Physics Journal (2005), V.48, N 7, P.694-700.

9. Isavnin A.G. // Russian Physics Journal (2006), V.49, N 3, P.308-313.

10. Isavnin A.G. // Russian Physics Journal (2007), V.50, N 5, P.471-476.