Надеев Е.И. инж., Калиниченко В.В. инж, Ганза А.И. инж.

Красноармейский индустриальный институт Донецкого национального технического университета, Украина

Деформация газожидкостного потока в эрлифте

Описывается процесс деформации газожидкостного потока в эрлифте.

The article describes the deformation process of the gas and liquid flour in the airlift.

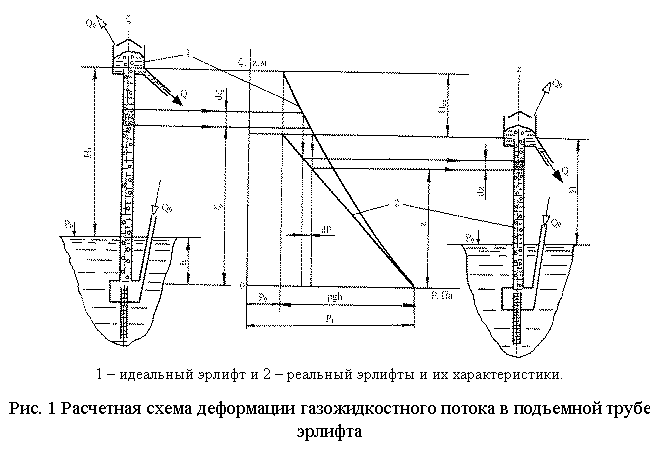
Исследование реального эрлифта будет неполным без учета деформации газожидкостного потока. Все научные исследования в этом направлении носят экспериментальный характер [1], [2]. Опытным путем установлен близкий к линейному закон распределения давления вдоль подъемной трубы эрлифта [2], что дает возможность провести теоретические исследования процесса деформации газожидкостного потока (рис. 1).

Сравним работу идеального и реального эрлифтов (рис. 1) с одинаковыми начальными параметрами: глубиной погружения h; диаметром подъемной трубы D; объемной производительностью Q; удельным расходом воздуха q0.

Под идеальным эрлифтом подразумевается эрлифт с отсутствием скольжения фаз и гидравлического трения при движении газожидкостной смеси. Теоретически установим закон изменения давления вдоль подъемной трубы идеального эрлифта и теоретическую высоту подъема жидкости. Изотермический газожидкостной поток смеси в подъемной трубе идеального эрлифта представим как гипотетическую, сплошную среду сжимаемой идеальной жидкости и запишем уравнение Бернулли в дифференциальной форме (рис. 1):

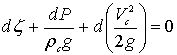, (1)

где: ζ – координата рассматриваемого сечения подъемной трубы идеального эрлифта, м;

Р – текущее давление в рассматриваемом сечении подъемной трубы эрлифта, Па;

ρс – плотность смеси в рассматриваемом сечении, кг/м3;

Vс – скорость смеси в рассматриваемом сечении, м/с;

g – ускорение силы тяжести, м/с2.

Плотность смеси ρс для идеального эрлифта определяется из равенства массовых расходов газожидкостной смеси и ее компонентов:

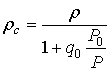, (2)

где: ρ – плотность жидкости, кг/м3;

q0 – удельный расход воздуха идеальным и реальным эрлифтами;

Р0 – давление при нормальных физических условиях, Па.

Удельный расход определяется:

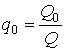, (3)

где: Q0 – расход воздуха, приведенный к нормальным физическим условиям, м3/с;

Q – подача воды, м3/с.

Скорость смеси есть отношение полного объемного расхода воздуха и жидкости к площади трубы S:

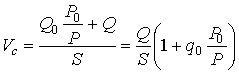(4)

Решаем совместно (1), (2), (4), получаем:

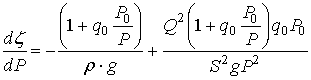. (5)

Проинтегрировав уравнение (5) при значениях параметров потока на входе в подъемную трубу эрлифта:

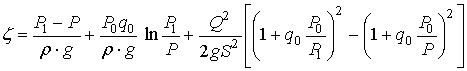(6)

Уравнение (6) устанавливает закон изменения давления вдоль подъемной трубы идеального эрлифта.

Процессы, протекающие в подъемной трубе реального эрлифта, будем рассматривать как квазиустановившиеся и параметры потока в любом сечении усреднены по времени. Рассмотрим влияние деформации газожидкостного потока на его геометрические параметры (рис. 1). Если произвести условное переключение идеального эрлифта на реальный, то вся газожидкостная смесь подъемной трубы идеального эрлифта разместится в подъемной трубе реального эрлифта, а масса смеси в элементарном объеме dζ идеального эрлифта равна массе смеси в соответствующем объеме реального эрлифта высотой dz:

, (7)

где: ρр – плотность смеси в реальном эрлифте, кг/м3.

Из рис. 1 следует, что закон изменения давления в реальном эрлифте по [2] носит линейную зависимость. Тогда:

, (8)

где: α – относительная глубина погружения.

Решая совместно (5), (7) и (8), получим:

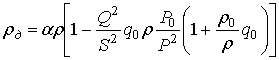(9)

Уравнение (9) отображает закон изменения плотности смеси только при учете деформации газожидкостного столба. При массовой подаче жидкости на много превышающей массовый расход воздуха составляющей можно пренебречь. Уравнение (9) примет вид:

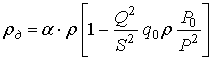. (10)

Площадь, занятая жидкой фазой, будет пропорциональна плотности смеси:

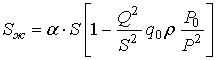. (11)

Площадь, занятая газообразной фазой, находится из уравнения:

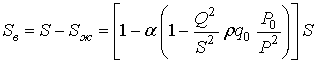(12)

Установим истинное (объемное) среднее по времени газосодержание, как среднюю по времени долю сечения трубы, занятую газовой фазой:

. (13)

После совместного решения уравнений (12) и (13) получим:

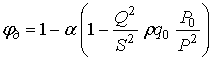(14)

Определим средние по времени скорости фаз в произвольном сечении:

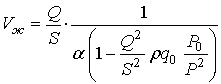(15)

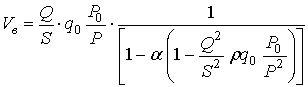. (16)

Коэффициент скольжения фаз при учете только деформации газожидкостного столба определиться как отношение скорости жидкой фазы к скорости газообразной фазы:

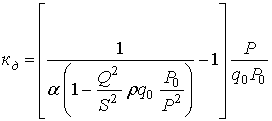. (17)

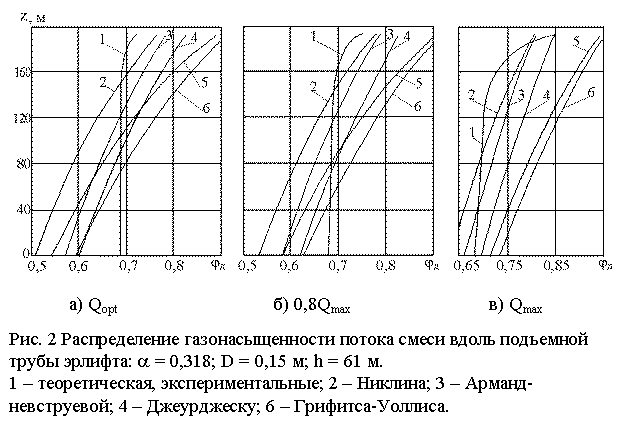
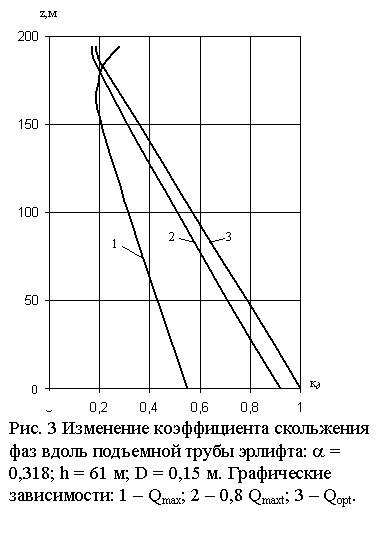
Из графиков на рис. 2 и рис. 3 следует, что при деформации газожидкостного столба коэффициент скольжения фаз – величина переменная, и чем ближе к устью эрлифта, тем он меньше. Но при Q_max он может возрастать (рис. 3), так как газожидкостная смесь представляет собой мелко дисперсную структуру. Теоретическая кривая 1 газо-насыщенного потока на рис. 2 пересекает область всех экспериментальных кривых и ни одной не подобна. Этот фактор указывает на то, что кроме явления деформации необходимо учитывать гидродинамику процесса движения жидкости.

Литература:

1. Арманд А.А., Невструева Е.И. Исследование механизма движения двухфазной смеси в вертикальной трубе. Известия ВТИ, №2, 1960 г.

2. Крылов А.П. Потери трения и скольжения при движении жидкости и газа по вертикальным трубам.