Пасічник
В.А.
(Дніпропетровський
національний університет ім. О. Гончара, Україна)
ДОСЛІДЖЕННЯ СТІЙКОСТІ ЗАЩЕМЛЕНОЇ ПО КОНТУРУ ПРЯМОКУТНОЇ ПЛАСТИНИ МЕТОДОМ
ЗБУРЕННЯ
Дослідження
стійкості пластин і оболонок представляє досить важливу з практичної точки зору
задачу, якій присвячена значна кількість наукових досліджень. Удосконалення методів
побудови розв’язків задач стійкості пластин зі змішаними крайовими умовами є
досить актуальною проблемою, що наполегливо розробляється в наукових
дослідженнях. На даний час найбільш широке застосування для
визначення критичних зусиль мають чисельні і наближені методи обчислень. Але
при цьому слід зазначити, що для змішаних випадків крайових умов закріплення
контуру пластини їх використання є досить складним для практичного застосування
і не дозволяє отримати задовільну точність обчислень. Особливість цих задач
полягає в тому, що характер хвилеутворення, змінність напруженого стану не є
попередньо заданими, а визначається як параметрами конструкції, так і
навантаженням. Тому розробка наближеного аналітичного методу розрахунку
критичних зусиль осьового стиску прямокутної пластини зі змішаними крайовими
умовами закріплення контуру є досить актуальною і має важливе практичне значення.
Тому для
розрахунку критичних зусиль осьового стиску прямокутної пластини з граничними
умовами защемлення контуру пропонується застосувати метод збурення виду
крайових умов та апроксимації Паде.
Розглядається прямокутна
пластину защемлена по контуру (–a/2£x£a/2; –b/2£x£b/2), яка
стискається в напрямку осі Оx силою N¢. Відповідне диференціальне рівняння у безрозмірному вигляді
запишеться так
![]() . (1)
. (1)
где N =N¢ b2/D, D – циліндрична жорсткість пластини, x= x/b, h=y/b, k=a/b.
Крайові умови для рівняння (1) запишемо у вигляді
![]() при
при ![]() , (2)
, (2)
![]() при
при ![]() . (3)
. (3)
При e = 0 реалізуються умови
шарнірного обпирання пластини по контуру, а при e = 1 – умови защемлення. Для проміжних значень ![]() реалізуються умови пружного
закріплення контура пластини з коефіцієнтом пружності m = e / (1-e ).
реалізуються умови пружного
закріплення контура пластини з коефіцієнтом пружності m = e / (1-e ).
Для побудови розв’язку крайової задачі (1) –
(3) у відповідності з методом збурення подамо
критичне зусилля ![]() і прогин пластини
і прогин пластини ![]() у вигляді асимптотичних рядів по параметру e:
у вигляді асимптотичних рядів по параметру e:
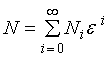 ;
; 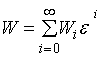 . (4)
. (4)
Підставляючи розкладення (4) у диференціальне
рівняння (1) і крайові умови (2), (3), в результаті застосування процедури
асимптотичного розщеплення за параметром e, отримуємо рекурентну послідовність крайових задач:
![]() :
: ![]() ,
(5)
,
(5)
![]() при
при ![]() , (6)
, (6)
![]() при
при ![]() . (7)
. (7)
![]() :
: 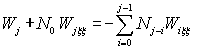 , (8)
, (8)
 при
при ![]() , (9)
, (9)
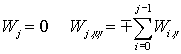 при
при ![]() . (10)
. (10)
Крайова задача нульового наближення
представляє собою задачу стійкості прямокутної пластини, яка стискається в
напрямку осі Ох поздовжнім зусиллям N0.
Враховуючи, що мінімальне значення критичного зусилля осьового стиснення N0 досягається при втраті
стійкості пластини з утворенням прямосиметричних форм, розв’язок задачі
нульового наближення записується так
![]() m, n = 1, 3, 5, ... . (11)
m, n = 1, 3, 5, ... . (11)
З урахуванням співвідношення (11) з крайової
задачі (5) (7) отримаємо значення критичного зусилля осьового стиску в
нульовому наближенні:
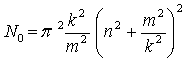 . (12)
. (12)
Аналогічно побудувавши розв’язки задач
першого та другого наближень отримуємо асимптотичний ряд для визначення
критичних сил осьового стиску:
![]() + … . (13)
+ … . (13)
Застосовуючи апроксимацію Паде для перших
трьох членів ряду (13) отримуємо остаточний розв’язок задачі осьового стиску
прямокутної пластини:
![]() . (14)
. (14)
Для оцінки
точності запропонованого підходу проведено порівняння отриманих результатів з
результатами чисельних розв’язків для квадратної пластини - N = 8,5540 p2. Відрізок асимптотичного ряду (13) при e = 1 дає значення
критичного зусилля осьового стиснення N = 5,4512 p2 (похибка – 56,9%), а розв’язок отриманий із застосуванням
АП (14) при e = 1 дає значення
– N = 7,8662 p2 (похибка - 8,04%). Аналіз отриманих результатів показує, що розв’язки
(13) і (14) для значень e 0,5 відрізняються
між собою менше ніж на 5%. Тому, значення параметра e = 0,5 можна вважати границею можливого застосування методу збурень.
Висновки. Таким чином, метод збурення виду крайових
умов в комплексі з апроксимацією Паде дозволяє побудувати ефективні розв’язки
задач визначення критичних зусиль для пластин, у разі, коли граничні умови
перешкоджають відокремленню просторових змінних. Застосування запропонованого
підходу дозволяє отримати якісну інформацію про можливі типи поведінки пластинчатих
конструкцій із задовільною точністю.