УДК 517.928.4:517.929.4

Технические науки/2.Механика

к.т.н. Дюсембина Ж. К.

Алматинский технологический университет, Казахстан

Динамика экологической системы и ее стабилизация на конечном интервале времени

Задача синтеза векторного управления из заданного класса для управляемых экологической системы и популяционной динамики сообщества с самолимитированием математическими моделями в виде квазилинейных уравнений.

_{Рассмотрим задачу управления вольтеровской системой:}

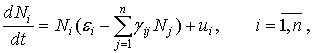₍₁₎

_{где вектор управлений выбирается из некоторого множества допустимых управлений:}

₍₂₎

_{Реально управление (2) имеют смысл только при}

_{При состояние равновесия определяется решениями уравнений}

_{Начало координат пространства представляет собой одно из положений равновесия. Предположим, что в системе (1) при существует положительное устойчивое состояние равновесия , определяемое уравнениями:}

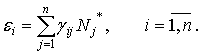₍₃₎

_{Рассмотрим задачу: найти такой вектор управлений , чтобы система (1) получила новое устойчивое положение равновесия >0.}

_{Таким образом, поставлена задача перевода состояния экологической системы на новый режим, при котором поддерживалась бы заданная численность популяций.}

_{Выберем в качестве допустимых управлений векторы вида}

₍₄₎

_где

_{Перепишем систему (1) в виде:}

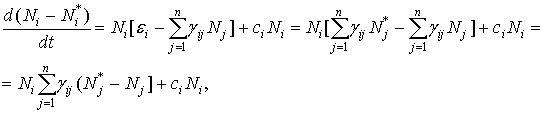
_т.е.

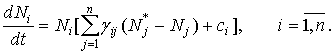₍₅₎

_{Найдем теперь исходя из условия, что система (5) имеет положение равновесия . Для этого необходимо, чтобы при выражение в скобках равнялось нулю. Отсюда получаем}

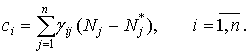₍₆₎

_{Таким образом, если в системе (1) управление выбирается в виде (4) с коэффициентами (6), то у нее появляется новое положение равновесия , причем устойчивое, если было устойчивым положение равновесия , поскольку на коэффициенты матрицы сообщества управление не оказывает влияния.}

_{В случае диссипативной системы при любом траектория системы (1) при выбранном управлении достигает точки в силу асимптотической устойчивости этого же положения равновесия. Таким образом, управления (4) с коэффициентами (6) в случае диссипативной системы решают задачу приведения системы (1) из любого начального положения в заданное стационарное состояние .}

_{В случае консервативной системы положение равновесия будет устойчивым, но не асимптотически. Поэтому в системе возникают устойчивые колебания численности, и задачу перевода в стационарное состояние управление (4) не решает.}

_{Рассмотрим функцию Ляпунова для консервативной системы (5) в виде:}

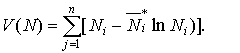₍₇₎

_{Производная этой функции вдоль траектории системы (5) имеет вид:}

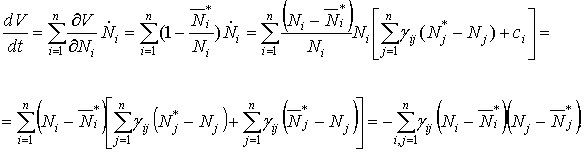₍₈₎

_{Поскольку рассматриваемая система консервативна, то производная функции вдоль траекторий системы тождественно равна нулю:}

_{Если заменим управление (4) на}

₍₉₎

_где

_,

_то

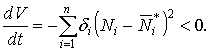₍₁₀₎

_{положение равновесия системы (1) при управлении (9) становится асимптотически устойчивым, и данное управление решает задачу перевода консервативной системы (1) в заданное устойчивое состояние равновесия .}

_{Литература:}

1. Меркин Д.Р. Введение в теорию устойчивости. – М.: Наука, 1976.

2. Алексеев В.В. и др. Физическое и математическое моделирование экосистем. – СПб.: Гидрометеоиздат, 1992.

3. Моисеев Н.Н. Модели экологии и эволюции. – М.: Знание, 1983.

4. Кадыров Х.К., Антомонов Ю.Г. Синтез математических моделей биологических и медицинских систем. – Киев: Наукова думка, 1974.