АнтропометрическАЯ моделЬ ПЕНТАКАНОНА

Ракчеева Т.А.

Институт машиноведения РАН, Россия, Москва

rta_ra@list.ru

Строение гармоничной фигуры тела человека подчиняется определенным закономерностям, связывающим элементы его скелетной конструкции в единое целое. Исследования норм структурной организации человеческой фигуры известны со времен Древнего Египта. Множество отдельных метрических соотношений, называемых канонами, дошло до наших дней. Кроме модульных, пропорциональных или шкальных канонов, известны примеры описания структурных свойств скелетной фигуры человека через вписывание ее в правильные геометрические фигуры, такие, как окружность, квадрат, пентаграмма. Конфигурационные связи, полученные таким вписыванием дают описание метрической организации фигуры человека на геометрическом языке, а соответствующие каноны являются конфигурационными. Вписывание в окружность или квадрат дает отдельные метрические связи для идентификации антропометрических закономерностей, но их число недостаточно для полного описания.

Настоящая работа посвящена формированию полного числа независимых конфигурационных связей при вписывании фигуры в пентаграмму. Множество полученных таким методом инвариантов составляет пентагональный конфигурационный антропометрический канон, который назван пентаканоном.

Процедура конфигурационного вписывания скелетной фигуры человека в пентаграмму позволяет получить полную систему антропометрических связей, достаточную для определения всех сегментов конечностей и тела.

Доказательством этого утверждения является система геометрических построений. Вписывание в пентаграмму производится элементарно только для дистальных 5-ти точек — головы, рук и ног, которые совмещаются с вершинами пентагона. Полное конфигурационное вписывание фигуры человека подразумевает поиск дополнительных точек, ассоциированных с геометрией пентаграммы, которые совместимы с точками суставов — внутренними точками многосегментной скелетной модели.

Традиционная схема антропометрических измерений (рис.1): H = v₁ — рост, v₂, v₃ — высоты подбородка и плеч; b_1, b₂, b₃ — уровни пупка, тазобедренного сустава (ТБС), лонного сращения (ингуинона); h₁, h₂, h₃ — уровни локтя, запястья, концов пальцев; l₁, l₂ — уровни колена, щиколотки; s₁, s₂ — ширины плеч и таза, s₃ — длина стопы.

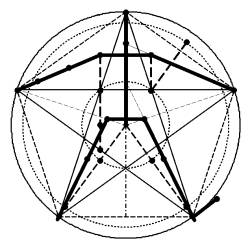
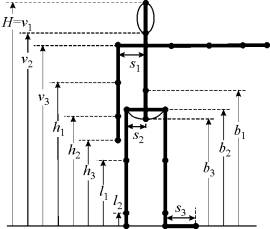
Рис.1. Измерительная схема Рис.2. Схема пентаканона

Процедура вписывания фигуры с «усредненными» антропометрическими данными в пентагон иллюстрирует рис. 2, где за единичный радиус круга принято расстояние от макушки до ингуинона. Выполненное вписывание воспроизводит оригинальный рисунок Агриппы. На этом этапе построения конфигурационного канона уже можно получить ряд метрических соотношений, как линейных, так и нелинейных, но целью являлись только линейные связи.

Рисунок Агриппы содержит, кроме окружности и фигуры человека, пентаграмму P₅, вписанную в пентагон p₅, и еще малый пентагон p₅. Характеристические параметры пентаграммы образуют следующее множество констант, используемое при построении пентаканона: С º {A, a, R_i, r_o, r_i}, где A = 2Rsina - сторона p₅, a = 8Rsinacos²2a - сторона p₅; R_i = Rcosa - радиус окружности, вписанной в p₅; r_i = Rcos2a и r_o = 2Rsinatga/2 – радиусы вписанной и описанной окружностей в p₅.

Из общей схемы конфигурационного канона пентаграммы (рис.2) видно, что суставные элементы руки приходятся на особые точки или линии пентаграммы. На основании этих соответствий сформируются остальные искомые связи пентаграммы и скелетной фигуры человека, которые легко формализуются в линейном виде. Полный вывод связей приведен в работах [1-2]. Выделенные связи в виде системы уравнений образуют полную линейную систему независимых инвариантных уравнений пентаканона, определяющих и синергии структурной организации фигуры человека.

Ниже приводится решение полученной системы уравнений пентаканона, в котором параметры измерительной схемы (рис.1) выражены через метрические параметры пентаграммы: A, a, R_i, r_o, r_i (список слева). Справа приведен соответствующий список параметров скелетной модели через известный параметр j, который является характерным для геометрии пентаграммы: j = (1+Ö5)/2.

v₁ = 2R ‑ Db; v₁ = R(5j ‑ 6)/2d;

v₂ = 2R ‑ r_oA²/(2R²) ‑ Db; v₂ = R(5j ‑ 2)/d;

v₃ = R + 2r_i ‑ Db; b₃ = R ‑ Db; v₃ = R7j/2d;

h₁ = 2R ‑ (r_i + r_o) ‑ Db; h₁ = R(5j + 1)/2d;

h₂ = R ‑ Db; h₂ = R(3j + 2)/2d;

h₃ = 2R ‑ (r_i + r_o) ‑ R(A/(2R_i))² ‑ Db; h₃ = R(15j ‑ 19)/2d;

l₁ = R ‑ r_o; l₁ = R(j ‑ 1);

l₂ = R ‑ r_o ‑ R(A/(2R_i))²; l₂ = R(5j ‑ 8);

s₁ = Ar_o/R; s₁ = R(2 ‑ j)Ö(3 ‑ j);

s₂ = 2ADb/r_o; s₂ = RÖ(3 ‑ j)/d;

s₃ = r_i, s₃ = R(j ‑ 1)/2,

где b₂ = R; Db = b₂ – b₃ = r_o²/(2R_i + 3r_o), j = (1+Ö5)/2, d = (j + 2).

Вычисленные таким образом параметры скелетной фигуры дают решение обратной задачи в явном виде. Они позволяют по одному параметру — радиусу или росту — рассчитать параметры обобщенной скелетной конструкции человека и размеры отдельных суставных элементов и построить антропометрическую модель. Система соотношений пентаканона, наряду с другими, исторически известными, канонами, прошла статистическую проверку на несмещенность и устойчивость (всего рассмотрено 32 соотношения).

Процедура конфигурационного вписывания исследуемой метрической структуры в другие структуры с известными метрическими свойствами, какими являются правильные (полуправильные) геометрические фигуры, порождает новый метод поиска структурных закономерностей ‑ структурную когнитивную графику.

Сравнительный анализ числа инвариантов, получаемых в результате вписывания в симплексы разных порядков от 3 до 8 показал, что максимальное число инвариантов дает пентаграмма, значительное их количество дает гексагональная структура, дальнейшее усложнение структуры не сопровождается увеличением числа инвариантов. Таким образом, выбор пентаграммы в качестве структуры для выведения полного числа инвариантов не случаен ‑ пентаграмма занимает особое место в ряду симплексных структур низких порядков [1, 2].

В заключение отметим, что скелетная модель, вписанная в пентаграмму, геометрически точными построениями может быть упакована во внутренний, малый пентагон p5 [1, 2].

Литература

1. Ракчеева Т.А. Pentacanon. // Фестиваль симметрии, Материалы. Будапешт, 2006.

2. Ракчеева Т.А. Пентаканон ‑ инварианты антропометрии. // Законодательная и прикладная метрология. №6(106)/2009.