Технические науки/ 6. Электротехника и радиоэлектроника

Стоцкая А.Д., Калинин А.В., Пекаровский А.С., Шелудько В.Н.

ГОУ ВПО Санкт-Петербургский государственный электротехнический университет, Россия

Исследование динамики ротора вращающегося в упругих опорах

Применение упругих опор – активных магнитных подшипников – в качестве подшипниковых узлов электрических машин в настоящее время является перспективным направлением в высокоскоростном машиностроении [1]. Рост скоростей вращения, требуемых для выполнения задач и технологических процессов промышленности, приводит к необходимости использования активных магнитных подшипников для стабилизации положения ротора электрической машины. Однако синтез системы управления активными магнитными подшипниками является сложной задачей вследствие наличия нелинейностей, присущих как самому ротору, так и магнитной системе подшипников.

Одной из задач при построении системы управления является исследование динамики объекта управления в определенном диапазоне скоростей вращения. В качестве объекта рассматривается ротор электрической машины, обладающий пятью степенями свободы.

Математическая модель ротора в упругих опорах имеет вид:

,

где – инерционная матрица, – матрица диссипативных и гироскопических сил, – матрица жесткости, – обобщенный вектор координат (рассматриваются координаты по осям X и Y, перемещения ротора относительно оси Z считаются пренебрежимо малыми), – вектор магнитных сил упругих опор (активных магнитных подшипников), – гравитационная сила, – обобщенная возмущающая сила [2]. Таким образом, исследуемый объект рассматривается как четырехканальная система.

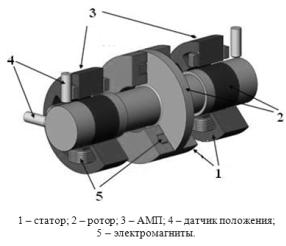Схематичное представление ротора в активных магнитных подшипниках имеет вид, приведенный на рис. 1.

Исследование объекта управления заключается в изучении свойств ротора при изменении скорости вращения. Рассматриваются различные характеристики объекта управления и дается оценка полученным изменениям.

Рис. 1 – Ротор в АМП

Влияние скорости вращения ротора на передаточные функции объекта. Для проведения исследования необходимо провести предварительную линеаризацию модели с целью получения передаточных функций каждого из четырех независимых каналов управления и рассмотреть динамику в рабочей точке.

Из анализа передаточных функций (ПФ) каналов следует, что с увеличением скорости вращения ротора изменяется их характер: если на малых скоростях вращения ПФ одного канала является комбинацией форсирующего звена 1-го порядка, апериодического звена 1-го порядка и колебательного звена

то на высоких скоростях (до 1000 рад/с) ПФ объекта является комбинацией форсирующего звена 1-го порядка, форсирующего звена 2-го порядка, апериодического звена 1-го порядка и двух колебательных звеньев:

.

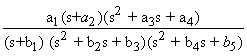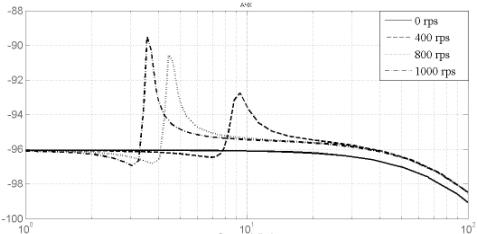
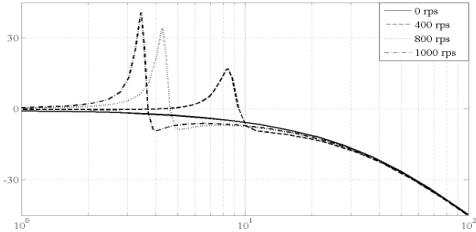
Переходные процессы, представленные на рис. 2, иллюстрируют влияние тех или иных звеньев на характер реакции системы. Как видно из рисунка с ростом частоты вращения, переходные процессы приобретают колебательный характер.

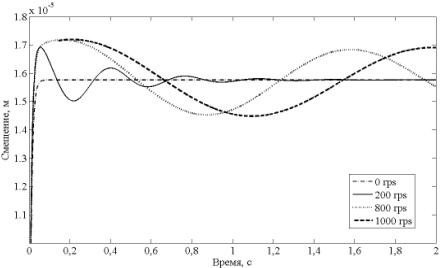
Рис. 2 – переходные процессы смещения ротора

Влияние скорости вращения ротора на расположение полюсов и нулей. Система строго собственная (реализуемая) – степень полинома числителя строго меньше степени полинома знаменателя [3]. При скорости вращения ротора равной нулю, полюсы и нули передаточной функции объекта управления лежат на вещественной оси, а с ростом скорости вращения ротора становятся комплекснозначными и сдвигаются к мнимой оси, что свидетельствует о том, что система стремится к колебательной границе устойчивости.

По расположению полюсов можно сделать следующие выводы о корневых показателях качества системы:

1. Показатель устойчивости η(ω) с ростом скорости вращения ротора уменьшается;

2. Показатель колебательности μ(ω) с ростом скорости вращения ротора увеличивается.

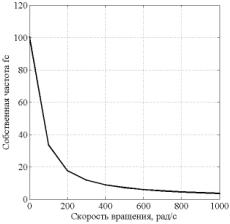
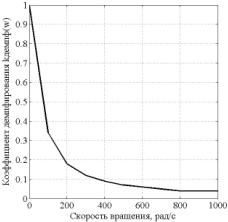
При этом необходимо отметить, что при увеличении скорости вращения, собственная частота затухающих колебаний экспоненциально уменьшается. Значения собственных частот f_с(ω) и коэффициента демпфирования k_демпф(ω) в зависимости от скорости ω представлены на рис. 3 и рис. 4 соответственно.

Рис. 3 – Зависимость f_с от скорости вращения ротора

Рис. 4 – Зависимость k_демпф от скорости вращения ротора

Влияние скорости вращения ротора на частотные характеристики объекта. Рассматривается семейство логарифмических амплитудных частотных характеристик (ЛАЧХ) (рис. 5) и фазовых частотных характеристик (ЛФХ) (рис. 6) модели объекта при изменении скорости вращения ротора от 0 до 1000 рад/. ЛАЧХ/ЛФХ модели объекта имеют резонансный всплеск типа резонанс/антирезонанс. При скорости вращения ротора равной нулю, ЛАЧХ/ЛФХ не претерпевают изменений, и резонанса нет. При увеличении скорости вращения ротора появляется резонансный пик на частоте, определяемой мнимой частью доминирующей пары полюсов. Порядок наступления резонанса и антирезонанса, а также амплитуда соответствующего пика, зависит от соотношения вещественных частей полюсов и нулей и, одновременно, мнимых частей полюсов и нулей.

Рис. 5 – амплитудная частотная характеристика объекта

Рис. 6 – фазовая частотная характеристика объекта

Исследование динамики ротора, вращающегося в упругих опорах показало, что объект обладает рядом особенностей, которые должны быть учтены при формировании закона управления и синтезе средств коррекции, а именно: увеличение показателя колебательности и уменьшение показателя устойчивости, а также появление резонанса на логарифмических амплитудной и фазовой частотной характеристиках объекта при вращении ротора.

Литература:

1. Журавлев Ю. Н. Активные магнитные подшипники: Теория, расчет, применение. СПб.: Политехника, 2003. – С. 206.

2. Меркин Д.Р. Введение в теорию устойчивости. – М.: Наука, 1971. – С. 312.

3. Проектирование систем управления/ Г.К. Гудвин, С.Ф. Гребе, М.Э. Сальгадо. – М.: БИНОМ. Лаборатория знаний, 2004. – С. 911.