Технические науки. Авиация и космонавтика.
А.Б.Бушуев, В.В. Григорьев, А.Н. Коровьяков, Ю.В. Литвинов
Санкт-Петербургский
Государственный Университет
Информационных Технологий Механики и Оптики
Оценка работоспособности измерителя
дальности
в посадочном комплексе БПЛА
В настоящее
время наиболее сложным является вопрос получения информации о положении летательного
аппарата (ЛА) относительно ВПП. Поэтому, для построения системы автоматической
посадки требуется решить следующие задачи [ 1,2]:
-
обеспечения информацией о положении ЛА относительно ВПП;
-
построения оптимальной траектории движения ЛА в процессе посадки;
-
оптимального управления стабилизацией ЛА на заданной траектории.
Оценка
влияния возмущений
Для
описания динамики работы автоматического измерителя дальности (АИД) в режиме
слежения, используем модель, представленную уравнениями состояния в виде [ 3,4]:
, (1)
,
где: х – вектор состояния модели АИД, у – вектор выходных переменных, F= А –В k -
матрица замкнутой АИД, С – матрица связи векторов у и x, w(m) – случайное
возмущение, действующее на АИД, матрица G определяет входы, по которым действует возмущение.
Рассмотрим
влияние на АИД случайного возмущения при условии движения цели с малой
скоростью, т.е. положим
M[x(0)] = 
(0) = 0,
где M[
] – операция взятия математического ожидания вектора х(0),
Пусть матрица ковариаций вектора начальных отклонений равна:
M[x(0) x
(0)] =X
.
Будем считать
возмущение скалярным случайным процессом w(m) с дискретным временем. Взяв математическое ожидание от выражения (1) получаем:
(m+1) =F
(m) + G 
(m),
(m) = C 
(m), (2)
Уравнение для поведения во времени матрицы
дисперсий АИД получим [3] следующим
образом:
= F
+ 
, 
= X(0), (3)
где 
= M [(x(m) – 
(m)) ( x(m)-x(m))
] -матрица
ковариаций (дисперсий) вектора состояний АИД.
Дисперсия
выходной переменной (изменения дальности) АИД определяется выражением
, (4)
Если ( 
) и замкнутая АИД асимптотически устойчива,
то решение 
матричного уравнения (3) сходится к
стационарному значению, являющемуся решением алгебраического матричного
уравнения
(5)
и определяет матрицу дисперсий в установившемся режиме.
Вероятность нахождения вектора состояний x внутри
эллипсоида
(6)
подчиняется
распределению
с n степенями
свободы, где n - размерность
вектора состояний АИД. Поверхность (6) называют эллипсоидом правдоподобия.
Значение вероятности нахождения вектора состояния АИД внутри эллипсоида
правдоподобия (6) удобно вычислять как значение функции 
распределения:
.
Эллипсоиды
правдоподобия с течением времени стремятся к постоянному эллипсоиду
, (7)
где матрица 
обратная матрица по
отношению к матрице X , определяемой из решения уравнения (5).
Стационарная «трубка»
равновероятностного уровня, построенная на основании соотношения (7)
характеризует установившийся режим работы АИД [5].
Введённые
«трубки» равновероятностного уровня,
представляют информацию о статических и динамических свойствах АИД в наглядной
графической форме (Рисунок 1).
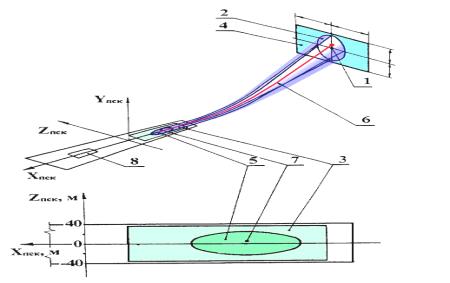
Рисунок 1.
1-точка входа в глиссаду; 2,4-области
допустимых отклонений при входе в глиссаду; 3-ВПП; 5-область
допустимых отклонений расчётной точки касания; 6-глиссада; 7-расчётная
точка касания; 8-область полной
остановки самолёта.
Заключение
Было
проведено математическое моделирование и построены «трубки» равновероятностного
уровня вектора состояний. Время сходимости процессов в АИД к установившемуся
режиму оценивается несколькими десятками интервалов дискретности Т, но в силу
его малого значения (Т=1/500=0,002 с)
это время оказывается вполне приемлемым
и оценивается величиной порядка 0,04 с.
Литература
1.
В. Зиновьев, А. Г.
Гузий . Информационные комплексы для автономных автоматических систем посадки , ВВИА им. проф. Н. Е. Жуковского, журнал
«Проблемы безопасности полетов», 08-2008
2.
Дудник П.И., Чересов
Ю.И. Авиационные радиолокационные устройства,
-М.:ВВИА
им проф. Н.Е. Жуковского, 1986
3.
Квакернаак Х., Сиван Р.
Линейные оптимальные системы управления.
-М.:Мир,
1977
4.
Брайсон А., Хо Ю-Ши.
Прикладная теория оптимального управления.
-М.: Мир,
1972
5. В.В.
Григорьев, Д.В.Козис, А.Н.
Коровьяков, Ю.В. Литвинов Анализ
поведения автоматических радиодальномеров при случайных возмущениях//Известия
Вузов.Приборостроение, №7, 2010.С.3-7
Сведения об
авторах:
1.
Бушуев Александр Борисович,
ГОУВПО «Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики», к.т.н., доцент.
Россия, Санкт-Петербург, Петергофское шоссе, д.11/21, кв.434.
р.т. (812) 595-41-28, д.т. (812) 745-30-81 Email: bushyev@inbox.ru
Bushyev Alexandr Borisovich, the senior lecturer of chair of
Control systems
and Computer science, the St.-Petersburg
State University Information
Technologies of Mechanics and Optics. Email:
bushyev@inbox.ru
2.
Григорьев Валерий
Владимирович.
зав. кафедрой Систем Управления
и Информатики,
ГОУВПО «Санкт-Петербургский
Государственный Университет
Информационных технологий Механики и Оптики»,
д.т.н., профессор , г.С-Петербург, ул. Ленина, д.50, кв.31,
р.т. (812) 595-41-28, д.т. (812) 235-55-34
Email: grigvv@yandex.ru
Grigoriev Valery Vladimirovich. The manager Control systems and
Computer science, the
St.-Petersburg State University Information
Technologies of Mechanics and
Optics, the professor,
Email: grigvv@yandex.ru
3. Коровьяков Анатолий Николаевич, доцент
каф. Систем Управления и Информатики,
ГОУВПО «Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики», к.т.н., с.н.с.,
г.С-Петербург, ул. М.Балканская, д.36, кор.1, кв.111,
р.т. (812) 595-41-28, д.т. (812) 771-65-35
Email: 06kan@mail.ru
Korovjakov Anatoly Nikolaevich, the senior lecturer chair of Control
systems
and Computer science, the
St.-Petersburg State University
Information Technologies of Mechanics and Optics, Email: 06kan@mail.ru
3.
Литвинов Юрий
Володарович, доцент кафедры Систем
Управления и
Информатики, ГОУВПО
«Санкт-Петербургский Государственный
Университет Информационных Технологий Механики и Оптики»,
к.т.н., г.С-Петербург, ул.Решетникова, д.3, кв.30
р.т. (812) 595-41-28, д.т. (812) 656-97-25
Email: yurl13@yandex.ru
Litvinov Jury Volodarovich, the senior
lecturer of chair of Control systems
and Computer science, the St.-Petersburg
State University Information
Technologies of Mechanics and Optics,
Email: yurl13@yandex.ru