Д.т.н., профессор. Пиль Э.А.,

Санкт-Петербург, Россия

РАСЧЕТ области ВВП ПРИ изменении трех ЗНАЧЕНИй переменных

В статье рассматриваются влияния трех переменных на область ВВП (GDPc2-1), в которой она может существовать. При этом переменные являются постоянными, увеличиваются или уменьшаются. То есть, в предлагаемой статье рассмотрена зависимость изменения GDPc2-1 = f(Х1, Х2, Х3), которые имеют две кривые верхнюю (кривая 1 - GDPc1) и нижнюю (кривая 2 - GDPc2) границы. Здесь следует отметить, что кривая GDPc1 при данном масштабе сливается с осью абсцисс.

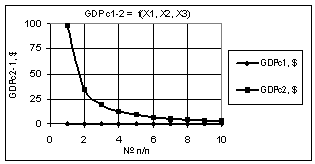
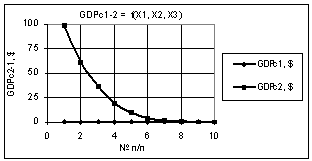
На первом рис. 1 показана зависимость GDPc2-1 при Х1 = Х2 = 1, Х3 = 1…10. Из данного графика видно, что зависимость GDPc1 постоянно уменьшается, начиная со значений 98 в начале и 3,1 в конце, т.е. ее значения уменьшились в 31,65 раз.

Рис. 1. GDPc2-1 =f(X1,X2,X3) Х1 = Х2 = 1, Х3 = 1…10

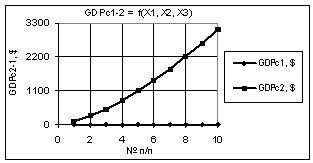
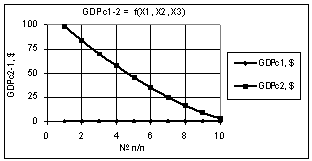
Рис. 2. GDPc2-1 =f(X1,X2,X3) Х1 = 1, Х2 = Х3 = 1…10

Следующий рис. 2 дает наглядное представление, что при увеличении двух переменных Х2 и Х3 в 10 раз значения экономической оболочки увеличиваются по степенной зависимости вида GDPc2 = 98,122x^1,5. при этом коэффициент корреляции равен R² = 1. Здесь построенная кривая имела следующие параметры Х1 = 1, Х2 = Х3 = 1…10.

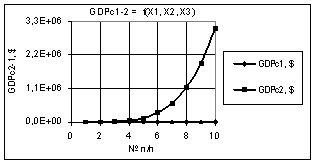
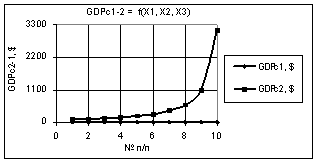
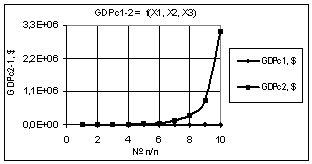
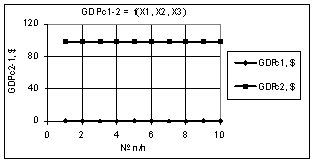
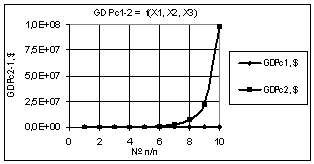
На следующих двух рисунках 3 и 4 показаны две зависимости GDPc2-1 = f(Х1, Х2, Х3), когда переменные были: Х1 = Х2 = 1…10, Х3 = 1 и Х1 = Х3 = 1…10, Х2 = 1 соответственно. Как видно из рис. 3 здесь, при данных значениях переменных, значения GDPc2 увеличивается очень значительно для рис. 3 в 3,16Е+4 раза, а для рис. 4 значения GDPc2-1 остаются без изменения 98,12 и 0,258.

Рис. 3. GDPc2-1 =f(X1,X2,X3) Х1 = Х2 = 1…10, Х3 = 1	Рис. 4. GDPc2-1 =f(X1,X2,X3) Х1 = Х3 = 1…10, Х2 = 1
Рис. 5. GDPc2-1 =f(X1,X2,X3) Х1 = Х2 = 1…0,1, Х3 = 1		Рис. 6. GDPc2-1 =f(X1,X2,X3) Х1 = 1…0,1, Х2 = Х3 = 1

Следующие два рисунка 5 и 6 были построены при Х1 = Х2 = 1…0,1, Х3 = 1 и Х1 = 1…0,1, Х2 = Х3 = 1. Здесь видно, что построенные кривые GDPc2 уменьшаются в обоих случаях. Так для рис. 5 уменьшение происходит по полиномиальной зависимости четвертой степени, а для рис. 6 по степенной зависимости.

Рис. 7. GDPc2-1 =f(X1,X2,X3) Х1 = Х2 = 1, Х3 = 1…0,1

Рис. 8. GDPc2-1 =f(X1,X2,X3) Х1= Х2 = 1…10, Х3 = 1…0,1

Для построения двух кривых на рис. 7 и 8 были использованы следующие значениях переменных Х1 = Х2 = 1, Х3 = 1…0,1 и Х1= Х2 = 1…10, Х3 = 1…0,1. Из рис. 7 видно, что увеличения GDPc2 происходят незначительно, в то время как для рис. 8 значения GDPc2 увеличиваются в 1,0Е+6 раз.

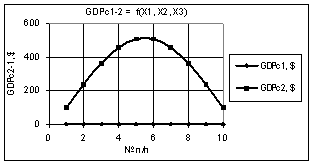
Построенная зависимость GDPc2 на рис. 9 при Х1 = 1…10, Х2 = Х3 = 1…0,1 получилась симметричной и имеет максимальное значении 5,88, при этом она увеличивается и уменьшается в 5,2 раза.

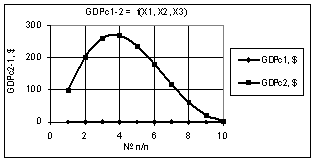
Из следующего рис. 10 видно, что построенная кривая GDPc2 при переменных Х1 = 1…10, Х2 = 1…0,1, Х3 = 1 имеет максимум 269,25 в точке 4, после чего уменьшается в 86,85 раза.

Рис. 9. GDPc2-1 =f(X1,X2,X3) Х1 = 1…10, Х2 = Х3 = 1…0,1

Рис. 10. GDPc2-1 =f(X1,X2,X3) Х1 = 1…10, Х2 = 1…0,1, Х3 = 1

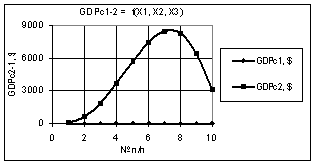
Рис. 11. GDPc2-1 =f(X1,X2,X3) Х1 = 1, Х2 = 1…10, Х3 = 1…0,1

Рис. 12. GDPc2-1 =f(X1,X2,X3) Х1 = 1…0,1, Х2 = 1…10, Х3 = 1

На последних двух рисунках 11 и 12 видно, что значения построенных кривых GDPc2 либо увеличиваются в 31594 раза (рис. 11), либо имеют максимум 14570 в точке 7, после чего уменьшаются до величины 3102,97 (рис. 12). Эти рисунки были построены, когда значения переменных были следующими: Х1 = 1, Х2 = 1…10, Х3 = 1…0,1 и Х1 = 1…0,1, Х2 = 1…10, Х3 = 1.