On software reliability
for organization of banking operations
The development of banking software is one of the promising areas of
modern IT market. Banking is experiencing its heyday, and every decade
determines its form and its inherent characteristics. The fast increase of
banks is promoted by the liberal policy for licensing banks. Each crisis reveals
the weakness of many banking services in the CIS countries: the high dependence
of banks on short-term government bonds, shadow ownership structure and degree
of credit risk. This situation shows the vulnerability of the banking sector.
The opening of new banks and development of the old ones require reforming of
the banking information system. And closing to standards accepted worldwide,
especially in Western countries. Building of information system means the
development of banking software for specific tasks, and in view of specific
requirements of the banking sector.
Software development is the process aimed at creation and maintenance of
performance, quality and reliability of processes. To achieve it are used
technologies, methods and practice of informatics, project management,
mathematics, engineering and other knowledge areas.
As other areas, the information technologies and processes deal with
problems of quality, cost and reliability. Of special note are the programs
containing millions of source code lines that, as expected, have to be executed
correctly in changing conditions. Complexity of software is comparable with
complexity of the most modern machines that are continuously improved.
Reliability of the banking software is the main problem of the
information system. Researches in the field of banking software are in the
stage of development, because the ratio of maximum and peak performance ranges
from 60% to 83%. An example is the company ORACLE that has bought the operating
system SOLARIS for optimization the applications, which works more quickly
using the cloud technology. The main objectives and indicators of the banking
software is the reliability of banking system and its software. Under the
reliability of banking software is understood the software capability to meet
the prescribed requirements. The quality of banking software is shown in joint
processing of hardware and software. It characterizes the unit’s capability to
perform the specified functions provided that the program will be in one state
or another.
Reliability of banking software reflects the qualitative status of the
program. Sometimes it is called a program correctness or program reliability.
Software reliability of the banking system is what interests the
consumer. To ensure it is necessary that the program is “correct”, “accurate”,
“reliable”, i.e. that it does not contain any errors. It may be that some
errors will never show up during the operation, or, on the contrary, in the
facility’s operation additional imperfections (“bugs”) of the program will be
discovered. But it is clear that the required condition of reliable operation
of the facility is the correctness of the software, i.e. absence of errors in
it.
Mathematical models allow estimating the errors’ characteristics in
programs and foreseeing the reliability of banking system in the course of
design and operation. Models are of probabilistic nature, and accuracy of
forecasts depends on accuracy of input data and forecasting depth over time.
Intensity of error detection in a program dn/dt and the absolute number of eliminated errors are bound by the equation:
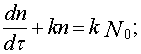where
k – coefficient.
Assumed that at the beginning of debugging by t=0 there are no detected errors, so the equation solution has the form:
The time between faults of programs before a failure T or non-failure
operating time being considered as the detectable distortion of programs, data
or computation process disturbing the performance is equal to the value inverse
of faults detection intensity:
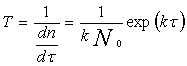
The
equation to calculate the proportionality factor:
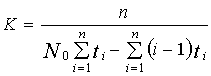
As a result, we can calculate the number of remaining errors in the
program and the mean time between faults Tñð
= 1/l. In debugging and testing programs,
to improve the time between faults from Ò1 to Ò2, it’s necessary to detect and eliminate Dn errors. The value Dn
is determined by the equation:
;
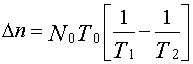The equation to determine the time Dt consumed for debugging that allows eliminating of Dn errors and accordingly increasing the time between faults from Ò1 to Ò2, looks as follows:
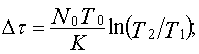
To estimate the time between faults we get the equation corresponding to
the Rayleigh distribution:
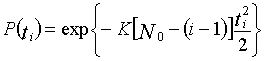
Exponential
model for distribution:
From
this, the distribution density of the time between faults T is determined by
the equation:
where t> 0, l> 0 and 1/l - mean time between faults, i.e. Òñð=1/l. Here Òñð is the mean time between faults.
To approximate the intensity change from time under detection and
elimination of errors used the following function:
;
If 0<b<1, the faults intensity will decrease while debugging or operation.
By this form of function l(t)
the distribution density of the time between faults shall be described by the
two-parameter Weibull distribution:
.
The Weibull distribution well reflects the actual dependences by
calculation of time between faults function.
REFERENCE
1.
Khlebnikov, À.À. Information technologies: Coursebook / À.À. Khlebnikov. - Ì.: KnoRus, 2014. - 472 p.
2.
Polovko À.Ì. Foundations of reliability theory. - Ì.:
Science
3.
Golinkevitch Ò.À. Applicable reliability theory. - Ì.: High school
4.
Fedotova, E.L. Information technologies and systems: Study guide / E.L.
Fedotova. - Ì.: PH FORUM, RDC INFRA-M, 2013. - 352 p.
5.
Shishonok N.A. è
äð. Foundations of reliability theory and operation of radio electronic
equipment. - Ì.: Soviet radio.
6.
Agaltsov V.P., Titov V.M., Informatics for economists: Coursebook. - Ì.: ÈÄ. "Forum": INFRA-M 2013-448 p.
7.
Kogalovskiy M.R. Advanced technologies of information systems. — Ì.: DMK Press; IT Company, 2003. — 288 p. — ISBN 5-94074-200-9.