Кабатаева Б.С.

Казахский Национальный университет имени аль-Фараби,

Алматы, Казахстан

О некоторой постановке задачи двухфазной фильтрации несжимаемой и несмешивающейся жидкости

Одной из важнейших задач повышения качества разработки и рационального использования природных ресурсов нефтяных месторождений является извлечение нефти. Поиск и реализация новых методов повышения нефтеотдачи пластов является одним из важнейших направлений в нефтедобывающей отрасли. При этом основными способами увеличения дебита эксплуатационной скважины являются заводнение пластов или вытеснение нефти оторочками из поверхностно-активных веществ, термическое воздействие, система газлифта и т.д. Однако достичь полного извлечения нефти или газа не удается. Это обусловлено рядом причин: сложностью поровой структуры пласта, его неоднородностью, действием капиллярных сил, влиянием смачивающих свойств пород, слагающих пласт и т.п.

Под фильтрацией понимают движение жидкости в пористой среде. Среда считается пористой, если она содержит значительное число пустот, размеры которых малы по сравнению с характерными размерами рассматриваемой среды. Количественной характеристикой пористости может служить отношение объема пор к общему объему

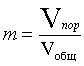(1)

Таким образом, пористость – величина безразмерная.

Учет пористости среды очевидным образом приводит к тому, что уравнение неразрывности для сплошного потока однородной жидкости

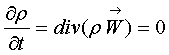(2)

примет вид

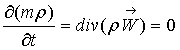(3)

где - вектор скорости фильтрации.

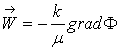(4)

где

(5)

В (1)-(5) - плотность, Р – давление, g- ускорение силы тяжести, Н- расстояние от рассматриваемой точки среды до некоторой фиксированной поверхности отсчета, - динамическая вязкость, к- проницаемость, т.е. проводимость пористой среды по отношению к данной жидкости. Проницаемость обратно пропорциональна сопротивлению, которое испытывает данная жидкость при течении сквозь данную пористую среду.

При вытеснении нефти из пласта водой имеет место задача фильтрации двух и более фаз несмешивающихся жидкостей. Рассмотрим совместное течение через пористую среду двух несмешивающихся жидкостей. Для определенности пусть будет нефть и вода. При таком течение часть пор будет занята водой, часть – нефтью. Насыщенность i-ой фазы определится как отношение объема пор, заполненных i-ой фазы, к общему объему пор :

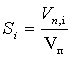, i=1,2 (6)

Из этого определения вытекает, что

(7)

При совместном течении многофазной несмешивающейся жидкости давления в каждой из фаз, вообще говоря, не равны между собой. Разность фазовых давлений есть так называемое капиллярное давление. В двухфазном течении оно определяется формулой Лапласа

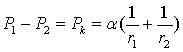(8)

где - главные радиусы кривизны поверхности раздела, в силу чего плоская поверхность раздела влечет за собой равенство фазовых давлений, - удельная свободная энергия поверхности раздела. Количественная ее характеристика – сила, действующая на единицу поверхности в тангенциальном направлении. Эту силу называют поверхностным натяжением.

Когда две различные несмешивающиеся жидкости заполняют поровое пространство, то угол, который образует поверхность раздела между двумя жидкостями с границей поры, определяется вторым законом Лапласа

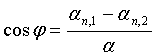(9)

Здесь - удельная свободная энергия поверхности раздела между i-ой жидкостью и границей поры, а угол отсчитывается со стороны второй жидкости. Пусть пористая среда первоначально была заполнена какой-либо одной жидкостью с поверхностным натяжением . Подведем к поверхности такой среды жидкость с поверхностным натяжением . Пусть >. Тогда в силу (10), угол - острый и подведенная жидкость будет как бы растекаться по поверхности пор, будет стремиться внедриться внутрь пористой среды, которая заполнена первой жидкостью, т.е. будет вытеснять первую жидкость. Поэтому статическое равновесие в пористой среде, заполненной двумя различными несмешивающимися жидкостями, возможно именно благодаря наличию капиллярного скачка (9). величина этого скачка естественно зависит от степени внедрения второй жидкости в пористую среду, заполненную первой жидкостью. Поэтому можно считать капиллярное давление функцией от насыщенности вытесняющей фазы.

(10)

Из приведенных выше рассуждений следует, что с увеличением насыщенности вытесняющей фазы величина капиллярного скачка, обеспечивающего статическое равновесие двух различных жидкостей в пористой среде, должна уменьшаться, т.е.

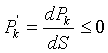(11)

Функция при заданных характеристиках пористой среды является для заданной пары жидкостей экспериментально измеряемой функцией. Боле точно, экспериментально измеряемой функцией является так называемая функция Леверетта J(S), связанная с капиллярным давлением следующим образом:

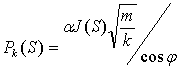(12)

Следует отметить, что при заданном значении насыщенности величина капиллярного скачка зависит, как показывает эксперимент, от способа замещения одной жидкости другой. Это явление носит название капиллярного гистерезиса. Его природу можно объяснить по-разному, для наших же дальнейших целей достаточно считать заданной функцией, удовлетворяющей условию (11).

Распространение закона Дарси на многофазное течение – не очень простая проблема. Ниже мы специально вернемся к этому вопросу, а пока будем предполагать, что справедлив так называемый обобщенный закон Дарси:

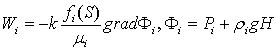(13)

Здесь - так называемые относительные фазовые проницаемости, которые, как и , являются экспериментально измеряемыми функциями насыщенности вытесняющей фазы.

(14)

Следует отметить одно очень важное обстоятельство. Существуют предельные значения насыщенности вытесняющей фазы такие, что при соответствующие фазовые проницаемости обращаются в нуль. Из (13) следует, что если , то неподвижна вытесняющая фаза, если же , то неподвижна вытесняемая фаза. При этом называют остаточной водонасыщенностью, - остаточной нефтенасыщенностью. С точки зрения физики процесса вытеснения достижение предельных значений соответствуют нарушению сплошности соответствующей фазы. А именно, когда , вторая фаза в суммарном течении присутствует лишь в виде отдельных островков, не связанных между собой. То же самое относится и к первой фазе при . Отметим также, что при капиллярными эффектами можно пренебречь. Это следует из вида кривой пропитки.

Далее договоримся считать как пористую среду, так и обе жидкости несжимаемыми. Тогда обычным образом, из условия сохранения массы каждой фазы, получаем уравнения, описывающие течение двухфазной несжимаемой жидкости в пористой среде:

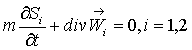(15)

К уравнению (15) нужно добавить (13) и соотношения (7), (10).

Литература:

1. Коновалов А. Н. Задачи фильтрации многофазной несжимаемой жидкости. - Новосибирск: Наука, 1988. - 166 с.

2. Bahaerguli Nulahemaiti, Guo Jindong, Ж.Д. Байшемиров. О некоторой постановке нестационарной фильтраций жидкости в упруго-пористом среде. Материалы международной конференции, Чехия – 2014. URL страницы: http://www.rusnauka.com/22_DNI_2014/Matemathics/4_174055.doc.htm

3. Антонцев С.Н., Монахов В.Н. О некоторых задачах фильтрации двухфазной несжимаемой жидкости // Динамика сплошной среды. 1969 г., Вып. 2.