Айдосов А., Зәуірбеков Н.С.,  Заурбекова Г.Н., Абсаматова Қ.А.

Алматы технологиялық университеті, Алматы қаласы, Қазақстан

жер үстіндегі атмосфера қабатында қоспалардың

таралу үрдісін Желдің айнымалы жылдамдығы кезінде модельдеу

 

Мақалада айнымалы жылдамдық кезінде болатын математикалық моделді құру қарастырылған. Ажырату әдісіне негізделген  алгоритмге сәйкес сандық есептеу бағдарламасы құрылған. Параметрлердің әртүрлі режимдері үшін қоспаның таратылуы алынған.

 

Нақты үрдіс айнымалы жылдамдық кезінде болады. Сондықтан айнымалы жылдамдық кезінде қоспалардың таралуының математикалық моделін құру қызықты. Бұл кезде есеп күрделенеді, себебі жылдамдық қандай заң бойынша өзгереді деген сұрақ туындайды, соған байланысты есепті шешудің ең тұрақты есептеу алгоритмінің түрі де күрделенеді, ЭЕМ-да алгоритмді орындау қиынға соғады. Бұл жұмыста нүктелік көздің қоспаларының таралу үрдісі зерттеледі. Облыс шекараларында және ХУ жазықтығында қоспа шамасы нөл деп алынады [1]. Есептің математикалық моделіне қорек көзі мүшесінің ауысу теңдеуі кіреді. Жеке туындыдағы дифференциалдық теңдеулерді қарастырайық:

,                  (1)

Бастапқы және шектік шарттарда:

,                             (2)

 және                                                      (3)

Мұнда  - қоспаның қарқындылығы; u,v,w – ОХ, ОУ, ОZ осьтері бойымен жылдамдық векторының құраушылары ;  - көлденең және тігінен тұтқырлық коэффициенті;  - негіздің өзара әрекет ету коэффициенті; a>0 – қоспаның төсеме бетпен өзара әрекеттесу коэффициенті;  - қоспа көзін сипаттайтын функция, оның түрі:

Мұндағы    - қоспа көзінің координаталары;  - қоспа көзінің іске қосылу уақыты;  Q – оның қуаты.

Шешімі   облысында ізделеді, мұнда: 

Жылдамдықтың айнымалы өрісі – қойылған есептерді шешуге белгілі бір ерекшеліктер енгізеді. (1)-(3) бастапқы дифференциалдық есептерді айырмалық есептермен аппроксимациялау кезінде қиындық туындайды. Жылдамдық айнымалы болған кездегі (1) өрнегіндегі сәйкес операторлардың аппроксимациясын қарастырайық. Бастапқыда конвективтік мүшелерден ғана тұратын тасымалдау теңдеулерін қарастырамыз, яғни екі өлшемді есепті [1-2]. Бастапқы теңдеуді келесідей жазамыз:

                                           ,                                                        (4)

Жалпы жағдайда жылдамдық құраушыларына x, y, z функциялары жатады. Бұл кезде әрбір t уақыт моментінде үзіксіздік теңдеуі орындалу керек

=0

(4) теңдеуін  түрінде жазайық, мұнда  

 Қарапайым әдіспен скаляр көбейтіндіні енгіземіз, яғни:

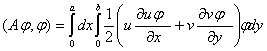
                                     (5)                                                 

Онда үзіксіздік теңдеуін ескеріп, (5) теңдеуін келесідей түрлендіруге болады:

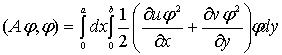                                  (6)

 

А=А1+А2 деп аламыз. Онда әрбір Аа(а=1,2) үшін:

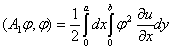
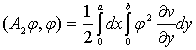             .                     (7)

Енді (7) теңдеуімен сипатталатын, бірақ операторлық теңдеу түрінде жазылған нақты үш өлшемді есепті  қарастырайық:

                                                                                              (8)

Бұған келесідей белгіленулер енгізілген:

;  ;

(8) теңдеуінің шешімін  облысында, келесідей бастапқы және шектік шарттар кезінде іздейміз:

;

;.                                                               (9)

Есепті сандық шешу үшін ажырату әдістеріне негізделген айырымдық сұлбаларын қолданамыз. Ажыратудың әртүрлі әдістері мен тәсілдері белгілі, мысалы, физикалық үрдістері бойынша, кеңістіктік айнымалылары бойынша. Біз қолданылған ажырату әдісінде, бірінші кезең көлденең тасымалдау  мен қоспа диффузиясынан тұрады, екінші кезең – OZ осьі бағытында конвекция мен диффузиядан тұрады. Бірақ, ажырату әдісінің қолданыла алатынына сенімді болу керек, яғни  бастапқы дифференциалдық есептің Аа анықталғандық  заңын тесеру керек, ол үшін   қатынасының орындалуын тексереміз. (7) шектік шарттарына сәйкес u=(z), v=const және w=const жағдайларын қарастырғанда, сонымен қатар u=(z), v=const және  w=const шарттарынан А1 операторының оң анықталғандығын аламыз.  Осы сияқты А2 операторының оң анықталғандығы туралы айтуға болады. Осы мақсатта  скаляр көбейтіндісін қарастырамыз, және оң анықталғандығы  шарты кезінде орындалады.

Біз  қоспаны ішінара жұту кезіндегі атмосферадағы лездік нүктелік көздің монодисперсті  белсенді емес қоспаның таралу есебін шештік. Оның математикалық моделі (6)-(7) теңдеулерімен көрсетілген. u жылдамдығының бойлық құраушысы – z координатасының функциясы. Жоғарыда айтылған ажырату әдісіне негізделген  алгоритмге сәйкес сандық есептеу бағдарламасы құрылған. Параметрлердің әртүрлі режимдері үшін қоспаның таратылуы алынған. Бойлық жылдамдықтың u=f(z) бастапқы түрі өзгерген, яғни Рейнольдс санының мәні. Облыста екі лездік тарату көзі болғандағы есептеулер жүргізілді. Белсенді емес монодисперсті  қоспаның таралу есебі сандық әдістермен шешілді. Алынған нәтижелер қарастырылып отырған ағынның физикалық заңдылықтарымен сәйкестеледі [3-4].

 

Қолданылған әдебиеттер тізімі:

1.   Айдосов А., Заурбеков Н.С. Теоретические основы прогнозирования природных процессов и экологической обстановки окружающей среды. Книга 3. Теоретические основы прогнозирования атмосферных процессов, экологической обстановки окружающей среды и построение геоэкологической карты на примере КНГКМ. - А., Қазақ университеті, 2000. (монография)– 219 с.

2.   Айдосов А., Заурбеков Н.С., Айдосов Г.А. Модельная оценка экологической обстановки окружающей среды при аварийных ситуациях.- Алматы, 2010 (монография). – 414 с.

3.   Айдосов А., Заурбеков Н.С., Айдосов Г.А. Модели экологической обстановки окружающей среды при реальных атмосферных процессах. - Алматы, 2010 (монография). –  368 с.

4.   Айдосов А.А., Айдосов Г.А., Заурбеков Н.С. Моделирование распространения вредных веществ в нижнем слое атмосферы со свободной верхней границей воздушной массы и оценка экологической обстановки окружающей среды.// Промышленность Казахстана. – Алматы. -  2007. -№1(40). - С. 68-70.