О.О.Бойко

Дніпропетровський національний університет ім.. Олеся Гончара

Реалізація алгоритмів кодування із знаходженням та виправленням однократної помилки. Код на контрольну суму та код Хеміннга.

Вступ. Передусім визначимося з тим, для чого саме потрібні коди з знаходженням та виправленням помилок. Як ми знаємо, що кожна інформація повинна десь зберігатись, а отже вона повинна пройти якийсь шлях до свого місця призначення. Однак саме при проходженні цього шляху й можуть виникати так звані помилки. Для того, щоб знайти їх та виправити використовують кодування. Коди поділяються на прості та складні. До простих кодів належать коди з мінімальними можливостями, а саме із знаходженням помилок. Складні ж коди здатні не тільки вказати на те що відбулась помилка, а й знайти її місце знаходження та виправити. Отже кодування існує для того, щоб при передачі інформації ми отримали її без пошкоджень, також відомо, що система усіх комп’ютерів складається з подвійної системи кодування, бо будь яку інформацію легше зберігати коли її описує лише два символи.

Аналіз останніх досягнень та публікацій. Згідно з останніх досягнень ми бачимо, що найбільшою популярністю користуються коди саме з виправленням помилок, однак для більш локальних проблем раціональніше використовувати коди більш нижчого типу. Прикладом застосування кодів з виправленням помилок при передачі інформації може слугувати CD/DVD приводи, в яких передача відбувається за допомогою коду Грея. Також коди з виправленням помилок використовуються при збереженні та передачіінформації в Інтернеті у таких протоколах як MD5, HTTPтощо. Отже ми бачимо, що коди із знаходженням та коди з виправленням помилок мають певне використання та задовольняють ті потреби які вимагає людина.

Постановка задачі.Визначивши для чого саме існують коди з знаходженням та виправленням помилок, розібрали їх види та можливості. Також детально розглянувши алгоритм Хеміннга ми обрали його, як приклад для ще більш кращого пояснення роботи кодів з виправленням помилок. Реалізація якого є головним завданням даного дослідження. Також головною метою даної роботи є доповнити статтю на сайті http://habrahabr.ru/ програмою, з якого і було знайдено інформацію про алгоритм Хеміннга який використовувався для написання програми.

Основні результати. Методика роботи. Для написання програми використовувалася мова програмування С, у програмному середовищі Dev C++.

Опис простого коду із знаходженням помилок.Прикладом простого кодування може слугувати код з перевіркою на парність. Принцип роботи якого полягає в тому, що до кожного слова в повідомленні, представлене у подвійнійсистемі числення, додається ще один символ(біт). Цей останній символ відповідає за суму інформаційних біт, тих що стоять перед останнім. Наступним чином вважаємо, що цей останній символ парний ( тобто дорівнює 0) чи навпаки непарний (дорівнює 1). При такому кодуванні швидкість передачі інформації велика, однак через достатньо неприємну розрідженість воно не здатне виправити жодної помилки. Декодування ж відбувається таким чином, що, якщо в прийнятому слові сума інформаційних біт парна то вважається, що помилок не було знайдено, в оберненому випадку він відмовляється від декодування. Важливо те, що при такому декодуванні декодер не звертається до пам’яті.

Опис складного коду з виправленням однократної помилки. Код Хеміннга.

До складних кодів належить алгоритм Хеміннга. Алгоритмів Хеміннга існує багато, однак ми розглянемо найпростіший з них на одному з інформаційних слів «habr».

Принцип цього алгоритму полягає в тому, що ми спочатку переводимо повідомлення у бінарний вигляд, та розставляємо контрольні біти за ступенем двійки. Також ми повинні вирішитись з довжиною інформаційних біт. Довжина нашого повідомлення складатиме 16 біт. Тобто дане повідомлення буде передаватися по частинам, а саме по дві латинські букви, оскільки один символ у бінарному вигляді має довжину 8 біт. На рисунках зображених нижче показано повідомлення у бінарному вигляді та розставлені контрольні біти, на першій частині нашого повідомлення.

Повідомлення у бінарному вигляді

Повідомлення з контрольними бітами

Далі ми повинні вирішити які біти вони повинні контролювати. Це робиться за допомогою певного правила, а саме: контрольний біт під номером N, контролює кожні наступніN біт через N біт, починаючи з позиції N.Детальніше показано нижче на рисунку.

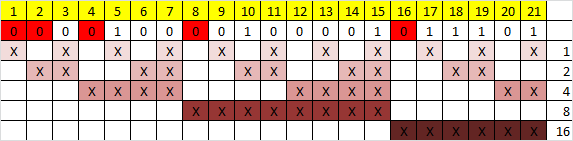
Тепер для того, щоб визначити значення контрольного біту ми повинні скласти ті контролюючі біти, які відповідають своїм контрольним бітам і отриману суму поділити навпіл. Якщо отриманий результат парний то контрольний біт дорівнюватиме 0,а якщо не парний то 1. Ось що ми отримали.

Тепер приступимо до фінальної частини алгоритму, а саме декодування та виправлення помилки.

Припустимо, що при передачі інформації виникла помилка, наприклад у 11 біті. Для того щоб її виявити ми повинні заново закодувати наше повідомлення, однак уже з помилкою. Отриманий результат порівнюємо з кодуванням повідомлення без помилки. Тепер коли ми порівняли повідомлення яке закодоване з помилкою і без помилки, додаємо ті контрольні біти які не співпадають і отриманий результат будет номером неправильного біта.

Закодовано без помилки

Закодовано з помилкою

З нашого прикладу ми бачимо, що біти під номерами 1,2,8 не співпадають. Склавши їх номера (1+2+8=11) отримуємо, що дійсно неправильним є 11-й біт. Тепер рекурсуємо його та відкинувши контрольні біти ми отримаємо наше початкове повідомлення.

Отже розглянувши приклад з виправленням однократної помилки, ми можемо підійти до основної мети, а саме реалізації цього алгоритму, за допомогою язика програмування С. Програма написана чітко за цим алгоритмом, а отже вона слугує, як приклад для наочного пояснення роботи даного виду кодування.

Код програми:

#include<stdio.h>

#include<MATH.h>

voidKoder_Dkoder (char a[])

{

charsum[5];

charbl[21];

int i,j,l,bufer;

for(i=0;i<=4;i++)//открылицкл для контрольныхбитизмасива сам

{

j=pow(2,i)-1;//контрольныебитырасставленные по степеням двойки в масиве а

//printf("j=%d\n",j);

a[j]='0';

bufer=j;

sum[i]=0;

while(bufer<=20)//цикл для масива а

{

for(l=bufer;((l<=bufer+j)&&(l<=20));l++)//цикл для одного блока контрольирующихбить одним контрольнымбитом в масиве а

{

if(a[l]=='1')

sum[i]=sum[i]+1;

}

/*printf("l=%d\n",l);*/

bufer=bufer+2*(j+1);// переход по блокам с котролирующимибитами в масиве а

}

}

printf("vivodnaekransumizavisimixbit\n");

for(i=0;i<=4;i++)

{//выводмасива сам на экран, тоесть результат суммыконтролирующихбитов для каждого контрольного бита

printf("sum[%d]=%d\n",i,sum[i]);

}

for(i=0;i<=4;i++)

{

j=pow(2,i)-1;

if(sum[i]%2==0) a[j]='0';

else a[j]='1';

}

// printf("Vvedenniyikodbilzakodirovan\n");

for(i=0;i<=20;i++)

printf("%c",a[i]);

}

main()

{

char a[21];

charbibik[21];

int i,j,b,t,T;

printf("Vveditekoddvuxbukv s kontrolnimibitami (dvjichnayiasistemaschisleniyia))\n");

for(i=0;i<=20;i++)

scanf("%c",&a[i]);

Koder_Dkoder(a);

printf("\nVveditenomershnura ");

scanf("%d",&b);

switch (b)

{

case 10: if(a[5]=='1') a[5]='0';

elseif(a[5]=='0') a[5]='1';

break;

case 15: if(a[10]=='1') a[10]='0';

elseif(a[10]=='0') a[10]='1';

break;

default:{}

}

for(i=0;i<=20;i++)

{printf("%c",a[i]);}

for(i=0;i<=20;i++)

{bibik[i]=a[i];

}

Koder_Dkoder(a);

printf("\nNomeranesootvetstvuishihbit\n");

t=0;T=0;

for(i=0;i<=20;i++)

if(bibik[i]!=a[i])

{t=t+(i+1);

T=t-1;

printf(" n=%d",i+1);}printf(" \nOshibka v %d bite",t);

if(bibik[T]=='1') bibik[T]='0';

elsebibik[T]='1';

printf("\n");

printf("Rekursirovali %d -yi bit i poluchiliobratnopraveliniyizakodirovaniyikod\n",t);

for(i=0;i<=20;i++)

{printf("%c",bibik[i]);}

printf("\n\n\KodeHemingmodelVer 1.1++");

getchar();

getchar();

}

Висновок. Після проведених досліджень ми виконали поставлену нами задачу. А саме розібрались для чого потрібне кодування та коди із знаходженням та виправленням помилок при передачі інформації по каналам зв’язку, чи перенесені її на диск або збереження на сайті у мережі Інтернет. Також доповнили готову статтю на сайті http://habrahabr.ru/ програмою. Отриманий продукт допоможе людям у вивченні алгоритмів Хеміннга і не тільки, адже цей алгоритм містить принципи простих кодів з задачею мінімуму. Також хочу зазначити, що програма була від лагоджена, одна я не упускаю той випадок, що її можна удосконалити. Так вона дійсно потребує удосконаленню однак на даному випадку те, що ми маємо може задовольнити головні вимоги які ми ставимо перед собою коли прагнемо вивчити алгоритм Хеміннга.

Література:

1. Код Хемінга. Приклад роботи алгоритму - https://habrahabr.ru/post/140611/

2. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер.с англ. М.:Мир, 1976, 600 с.

3. Пенин П.Е., Филиппов Л.Н. Радиотехнические системы передачи информации. М.: Радио и Связь 1984, 256 с.

4. Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. М.:Мир, 1986, 576 с.