Магистрант Туктубаева А.С.,

научный руководитель, к.т.н., Узденбаев Ж.Ш.

Жетысуский государственный университет имени И.Жансугурова,

г. Талдыкорган, Республика Казахстан

Моделирование компьютерных систем как задача многокритериальной оптимизации

Компьютерные системы является сложной средой, которая обслуживает произвольный запрос любого приложения. При этом могут быть использованы широкий спектр средств и способов. Поэтому задачи конвергенции и формирование универсальной инфраструктуры является одной из актуальных вопросов современных компьютерных корпоративных систем. Основу их построения можно представить в виде иерархической системы задач и их комплексной оценки в виде информационно – логической структуры как на рисунке 1. Она содержит следующие основные компоненты:

K = {K1, K2, …, KU, K0}; G={G₁={g₁₁, g₁₂,…, g_1N1}; G₂={g₂₁, g₂₂,…, g_2N2};…G_U={g_U1, g_U2,…, g_UNU}} - множества координирующих параметров для локальных задач нижестоящих уровней, например, системные, режимные параметры, трафик, уровни прерываний и назначение приоритетов, определение статуса доступа и т.д.;

M = {M₁={m₁₁, m₁₂,…, m_1N1}; M₂={m₂₁, m₂₂,…, m_2N2};… M_U={m_U1, m_U2,…, m_UNU}} - множества показателей для проектирования в задачах низшего уровня: отказоустойчивость, аппаратная совместимость, пропускная способность, поддерживаемые стандарты приема- передач, решений по созданию локальных контуров (подсетей), возможность автоматической автономной/ удаленной диагностики и т.д.;

D = {D₁={d₁₁, d₁₂,…, d_1N1}; D₂={d₂₁, d₂₂,…, d_2N2};… D_U={d_U1, d_U2,…, d_UNU}}; H = {H₁={h₁₁, h₁₂,…, h_1N1}; H₂={h₂₁, h₂₂,…, h_2N2};… H_U={h_U1, h_U2,…, h_UNU}}; P={p₁, p₂,…, p_U, p₀}- множества решений локальных задач: уровни мониторинга и управляемости, выбор технологических процедур и средств по обработке и передаче, способы, режимы приема- передач, проверка достоверности передаваемых/ принимаемых данных и их коррекция, способность восста

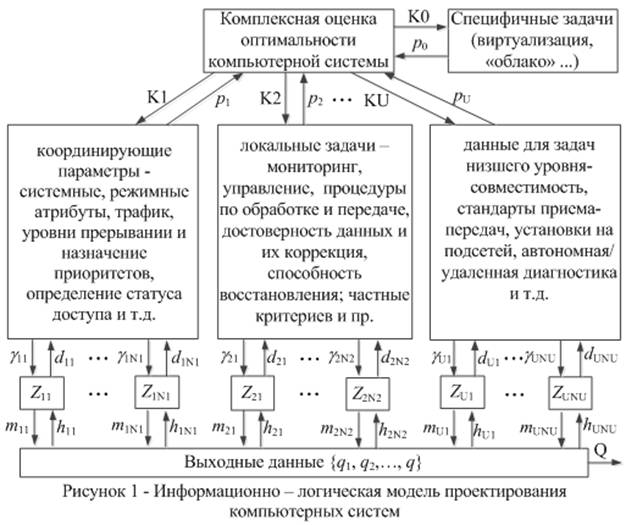
новления; значения критериев локальных задач оптимизации и др.;

Z = {Z₁={z₁₁, z₁₂,…, z_1N1} – множество модулей преобразований данных;

Q={q₁, q₂,…, q_J} - множество решений задачи построения компьютерной системы.

Таким образом, качество решений задачи создания системы оценивается не единственным критерием или показателем качества, а совокупностью критериев. Наличие множеств различных критериев оптимальности приводит к необходимости использования методов многокритериальной оптимизации [1,2]. При этом в каждом конкретном случае решаются проблемы выбора: альтернативных вариантов; методов решения задачи с учетом оценки вариантов по всем рассматриваемым критериям; принципа нормализации, приводящего все критерии к единому масштабу измерения и позволяющего проводить их сопоставления; принципа учета приоритета, позволяющего отдавать предпочтение более важным, по оценкам заказчика, критериям.

В формализованном виде задача проектирования компьютерной системы заключается в поиске минимума целевой функции F(w)

(1)

при выполнении следующих ограничении:

- детерминированных ограничений на выходные переменные

(2)

- функциональных ограничений

; (3)

- ограничений на значения показателей технологических процессов систем

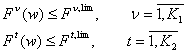(4)

операторов, описывающих математические модели принятия решения

здесь w_i*, с_j* , w_i** , _Сj** - соответственно, минимальные и максимальные значения в ограничениях (2) и (3); f_j (°) — некоторые функции от w₁, w₂, ..., w_n, заданные в явном виде; F^v(w), F^t(w), F^v,lim , F ^{t, lim} - значения показателей процессов обработки, преобразования (аппаратные, программные характеристики, весовые коэффициенты оценок и т. п.) и их заданные значения; К₁, К₂ — соответственно число показателей, для которых задается условие (4); - функциональный оператор; A_lm — множество данных; L_1, L_2, L ₃ — число функциональных операторов.

Из-за высокой размерности такие задачи разбиваются на ряд подзадач меньшей размерности и обобщенный критерий F(w) можно записать как

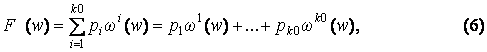
где p₁, ..., р_k0 — весовые коэффициенты,

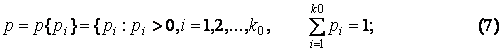
- взвешенные потери по i-му критерию;

- монотонные функции преобразующие каждую функцию цели к безразмерному виду

где и – соответственно наибольшее значение минимизируемых

и наименьшее значение максимизируемых функций F^k(w), на множестве допустимых альтернатив W;- оптимальное значение функции цели . Значения лежат в пределах от 0 до 1.

Для выбора единственного решения в задаче принятия сложного решения требуется задать весовые коэффициенты Pi, удовлетворяющие соотношению (7) и отражающие относительную важность функции цели …,, [1].

Для формализованного описания информационных массивов данных, необходимых для решения описанных выше задач, создается структурированная база данных. Она отображается информационно - логической моделью рассматриваемого класса и представляет собой объединение множеств данных, локальных моделей и связи между ними. Каждая локальная модель, в свою очередь, описывается кортежем аналогичной формы. В настоящее время существует различные способы решения многокритериальных задач [1,2,3].

В тех случаях, когда количество вариантов невелико искомое решение можно находить методом перебора вариантов. При более высокой размерности задача может быть упрощена путем последовательного анализа и отсеивании части элементов. Например, варианты (локальные задачи) разбиваются на категории в зависимости от количества используемых в дальнейшем выходных переменных по правилу: где r — коэффициент важности задаваемый разработчиком, для формирования приемлемых значений локального критерия F; F^h — значение критерия для h-го варианта формирования значений выходных переменных; Н — множество их допустимых значений.

Заключение

Предложен способ представления многокритериальной задачи построения компьютерных систем в виде структурированной по информационно – логическим признакам иерархической модели. Такой подход позволяет декомпозировать задачу, создает модульность и придает гибкость в организации стратегии проектирования.

Литература

1 А.Г.Трифонов. Многокритериальная оптимизация. Интернет ресурсы. http://matlab.exponenta.ru/optimiz/book_1/16.php.

2 Энциклопедия по машиностроению XXL. Задача многокритериальной оптимизации. Интернет ресурсы. http://mash-xxl.info/info/42819/.

3 Шоробура Н.Н. Разработка моделей и программных средств для многокритериальной оптимизации сложных объектов в компьютерных информационных системах. Автореферат магистерской диссертации. Интернет ресурсы. http://masters.donntu.org/2004/kita/shorobura/diss/index.htm.