О формировании размера заказа (на основе использования EOQ)

Ескендирова Д.М., Хаймулдина А.

Склады сырья, полуфабрикатов и готовой продукции являются одним из важнейших элементов любого производственного предприятия, а задача управления складом - классической задачей управления запасами и центральным объектом исследований теории управления и промышленной логистики.

Существуют две крайности при решении проблемы оптимальной партии заказа: делать очень редко заказ с большим количеством сырья, или частые заказы с малым количеством сырья. В первом случае минимальны затраты на оформление, доставку и т.д. партии заказа, но максимальны при хранении сырья. Во втором случае все наоборот. 
Задача логистики закупок и управления запасами заключается в бесперебойном обеспечении предприятия материальными ресурсами, отвечающими установленным стандартам качества, с наименьшими общими затратами и издержками на движение материалопотока включающими: номинальную цену, затраты на доставку, расходы на содержание запасов и иные выигрыши и потери. Одним из важных инструментов оптимизации управления запасами является расчёт оптимального размера поставки. А среди моделей расчёта особо выделяется формула Вильсона, которую также часто называют формулой оптимального размера заказа или формулой экономичного размера заказа (Economic order quantity – EOQ). 
Создание модели EOQ явилось толчком к распространению идей научного менеджмента в сфере управления логистическими процессами в производственном и торговом бизнесе. Впоследствии она была положена в основу математической теории запасов. Несмотря на широкую известность данной модели, история ее создания по-прежнему представляет собой загадку для большинства исследователей. Модель, впервые предложенная Ф. Харрисом в 1913 г. и развитая Р. Уилсоном в 1934 году, минимизирует в простейших предположениях суммарные затраты на хранение и пополнение товара[1]. 
Модель EOQ, которую часто называют формулой Уилсона, является простейшей оптимизационной моделью для детерминированного спроса, и отсутствия дефицита. Многие специалисты по логистике и преподаватели логистики считают ее простой, популярной, но сами нередко отказываются от её применения, указывая ту причину, что эта формула имеет ряд серьёзных ограничений и допущений. Допущения для формулы оптимального размера поставки EOQ следующие: 

расход ресурсов непрерывный и равномерный; 

период между двумя смежными поставками постоянен; 

спрос удовлетворяется полностью и мгновенно; 

транзитный и страховой запасы отсутствуют; 

ёмкость склада не ограничена;

затраты на размещение и выполнение заказа не зависят от размера заказа и постоянные в течение планового периода; 

цена поставляемой продукции в течение планового периода постоянная; 

затраты на содержание запаса единицы продукции в течение единицы времени постоянные и не зависит от суммы вложенных в запасы средств и сроков. 

Приведённые выше допущения накладывают много ограничений практического характера, без которых достоверность расчётов по данной формуле вызывает серьёзные сомнения. 

Для преодоления некоторых ограничений предпринимались попытки изменить алгоритм расчётов. С изменением алгоритма стал возможен анализ системы скидок, вариант формулы с пополнением запасов в течение некоторого времени, расчёт размера поставки в преддверии ожидаемого повышения цен на закупаемый товар. 

Однако без ответа остаются многие вопросы и среди них следующие: как рассчитать размер заказа, если доставку осуществляет поставщик и стоимость доставки включена в цену товара, как учесть наличие страховых запасов на складе, использовать ли в расчётах цену материалов с налогом на добавленную стоимость (НДС) или без НДС и т.п. Эти и тому подобные практические вопросы могут поставить специалиста по логистике в тупик, усомниться в действенности модели и отказаться от применения основного инструмента оптимизации поставок. 

Возможность применения модификаций формулы Вильсона для случаев, когда пополнение запасов осуществляется не мгновенно, а за определённый промежуток времени, для случаев предоставления системы скидок в зависимости от объёмов поставки и для случаев ожидаемого повышения цены на ресурсы достаточно известны, их описание можно найти во многих источниках. В данной статье они будут исключены из рассмотрения, но рассмотрим следующие три: влияние страховых запасов на расчёт оптимального размера поставки, уточнение переменных расходов, связанных с содержанием запасов и решение вопроса об используемой цене материальных ресурсов. 

Анализ разработанных математических моделей показал, что они позволяют учесть большинство факторов и разнообразие особенностей для каждого из типов задач управления запасами. Однако это же разнообразие привело к тому, что до сих пор для каждого реального производства приходится разрабатывать специальные модели, учитывающие именно его особенности и адаптированные к конкретным задачам данного производства.

Функционирование предприятий и организаций, так или иначе, связаны с задачами управления запасами, что говорит о необходимости научного подхода к управлению ими. Для научного управления запасами необходимо правильно представлять себе роль и значение запасов, факторы и их образования, мотивы их создания.

Наиболее распространенным инструментом в управлении запасами, направленным на минимизацию суммарных затрат, традиционно признается модель оптимального размера заказа (EOQ). Причиной популярности этой модели является как простота математического аппарата, так и хорошие результаты ее практического использования.

Проблема управления запасами в данной модели сведена к определению объема заказа (Q) и частоты выполнения заказов (T) за планируемый промежуток времени. Что в свою очередь рассчитывается посредством балансирования между затратами, связанными с выполнением одного заказа (O), и затратами на хранение единицы запасов (C). Размер заказа следует увеличивать до тех пор, пока снижение затрат на заказ перевешивает увеличение затрат на хранение [2].

В наиболее простом варианте модели, величина заказа и период между поставками принимаются постоянными величинами. Введенное в модель дополнительное ограничение по единовременной поставке новой партии в момент завершения запасов предыдущей, позволяет утверждать, что средний объем хранящихся на складе материалов равен Q/2. Соответственно, издержки хранения запасов за период между двумя поставками равны произведению затрат хранения единицы материала на средний объем запасов (рисунок 1.1)

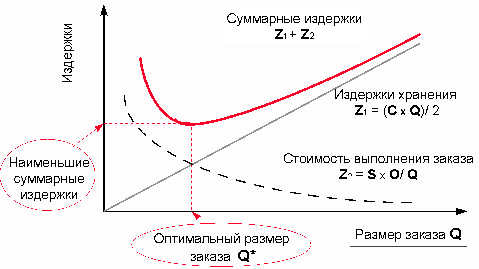
Рисунок 1.1 - Издержки хранения запасов

Для расчета затрат по выполнению заказа к условию неизменной величины заказа прибавляется предположение о постоянной стоимости заказов, поэтому затраты по заказу определяются как произведение затрат на один заказ и количество заказов за отчетный период (S/Q). Где S - это потребность в материалах или готовой продукции за отчетный период, а Q – объем заказа.

Оптимальный размер заказа получается при минимальных суммарных издержках по управлению запасами по формуле (1.1)

(1.1)

Приравнивая первую производную от функции суммарных затрат к нулю находим непосредственное значение оптимального размера заказа по формуле 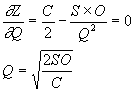(2.2)

(2.2)

Наиболее критичным фактором для эффективного использования модели является возможность оценить затраты на заказ и расходы ан хранение. Причем необходимо выделить именно переменные части затрат от заказа и единицы хранения запасов. Если пытаться провести выделение с достаточно высокой степенью точности, то скорей всего результаты будут неутешительными - переменные затраты составят незначительную часть от совокупных расходов на хранение или доставку, которые, в свою очередь, очень трудно выделить из общехозяйственных расходов [3,4].

Доскональное исследование проблемы выделения переменных затрат скорей навредит управлению, чем предоставит необходимую информацию. При работе с фактическими или плановыми данными необходимо постоянно балансировать между точностью и уместностью получаемой информации, не забывая, конечно, и о стоимости этих работ. Именно эти условия приводят к различной эффективности от использования модели на каждом отдельном предприятии. А причины возможных неудач зачастую скрыты не за спецификой производства, а за недостатком аналитических навыков и умений.

Список литературы

1. Стерлигова А.Н. Управление запасами в цепях поставок: Учебное пособие/-М.: Инфра-М, 2007. – 400 с.

2. Кремер Н.Ш. Исследование операций в экономике, М.:Юнити, 2002.- 407 c.

3. Хедли Дж., Уайтин Т. Анализ систем управления запасами, перев. с англ., М.:«Наука», 1999. - 511 c.

4. Модели и методы теории логистики: Учебное пособие. 2-е изд. / Под ред. проф. В.С. Лукинского. – СПб.: Питер, 2007. – 448 с.